方針
理論編で整理した内容の再現を基本とします。ゆえに断りなく理論編で用いた変数を使用します。
事前分布はJZSの事前分布のみ試します。というものこの理論の先駆者であるRichard D. Moreyさんが開発しているBayesFactorパッケージではJZSの事前分布を用いており、氏もこちらを推しているようなので。
本記事で検証する仮説は以下3組です。$\delta$はスケーリングされた平均値の差と解釈できる値で、ベイズ版平均値の差の検定で着目する値になります。
対応のある検定を実践
サンプルデータの可視化
データはこちらよりダウンロードできます。d$preは対策A実施前の交差点における事故発生件数、d$proは対策A実施後の交差点における事故発生件数とします。
load("data.RData")
head(d)
## pre pro
## 1 32 38
## 2 25 26
## 3 29 33
## 4 30 25
## 5 31 30
## 6 32 33
これらの差をとり、可視化してみます。 視覚的にはなんと対策前の事故件数の方が多そうです。しかし可視化で分かるのは「多そう」に留まってしまいます。対策前の事故件数の方が本当に多いと言えるのか、さらに深掘ってみましょうか。

可視化コードはこちら。
p <- d %>% as.data.frame() %>% mutate(D = pre - pro ) %>% select(D) %>% ggplot(aes(x=D)) + geom_histogram(breaks=seq(min(d$pre-d$pro)+0.5,max(d$pre-d$pro)+0.5,1), fill="#4169e1") +
theme_light(base_size=12) + xlab("pre - pro") + ylab(NULL)
両側検定
筆者は本分析よりStanの実行環境を「Windows + Rstudio Desktop + rstan」から「Ubuntu(Linux) + Rstudio Server + cmdstanr」に移行しました。 rコード・Stanコードとも現在のrstanではエラーが起きるので留意を。
Stanコードを示します。
//model1.stan
//One-sample t-test
data{
int N; //Common sample size
array[2] vector[N] D_raw; //Raw data
real<lower=0> r, Jeffreys_alpha, Jeffreys_beta;
//r:scale factor
//Jeffreys_alpha : mean of prior(sigma^2) (sufficiently small values)
//Jeffreys_beta : variance of prior(sigma^2) (sufficiently small values)
}
transformed data{
vector[N] D; //X - Y
D = D_raw[1] - D_raw[2];
}
parameters{
real delta; //effect size
real<lower=0> sigma, g;
}
model{
//Likelihood
target += normal_lpdf(D | delta * sigma, sigma);
//JZS prior
target += normal_lpdf(delta | 0, sqrt(g));
target += inv_gamma_lpdf(g | 0.5 , (r^2)*0.5);
target += gamma_lpdf(sigma^2 | Jeffreys_alpha, Jeffreys_beta);
}
generated quantities{
real mean_delta, variance_delta;
//mean_delta:mean of CMDE(delta)
//variance_delta:variance of CMDE(delta)
real BF_01;
// real BF_10;
real logPostDensDelta, logPriorDensDelta;
//logPostDensDelta:p(delta=0 | prior)
//logPostDensDelta:p(delta=0 | posterior)
mean_delta = sum(D) / (sigma * (N + (1 / g)));
variance_delta = 1 / (N + (1 / g));
logPostDensDelta = -0.5 * log(pi() * variance_delta * 2) - 0.5 * mean_delta^2 / variance_delta;
logPriorDensDelta = -log(pi() * r);
BF_01 = exp(logPostDensDelta - logPriorDensDelta);
//BF_10 = exp(logPriorDensDelta - logPostDensDelta);
}
筆者の見解では、$BF_{01}$及び$BF_{10}$のうち、1より小さい値をとる方をgenerated quatities{}で推定するのが精度の都合上よさそうです。というのも1より大きい値をとると考えられる$BF$は、正の方向に分布の裾が重くなってしまい、平均値が大きい値に引っ張られてしまうから。また$\mathbb{E}[BF_{01}] = \cfrac{1}{\mathbb{E}[BF_{10}]}$は成り立たないので、$BF_{01}$と$BF_{10}$のMCMCサンプルを同時に得ることもおすすめしません。データに応じてreal BF_01 とreal BF_10を使い分けましょう。
これを走らせるコードが以下です。
library(cmdstanr)
library(rstan)
library(tidyverse)
stan_data <- list(D_raw=t(d), N = nrow(d), r =sqrt(2)/2, Jeffreys_alpha=1e-10, Jeffreys_beta=1e-10)
model1_c <- cmdstan_model("/model/model1.stan")
fit_c1 <- model1_c$sample(
data = stan_data,
parallel_chains = 4,
chains = 4,
iter_warmup = 1000,
iter_sampling = 20000
)
収束を確認し、ベイズファクターを計算しましょう。
stanfit1 <- rstan::read_stan_csv(fit_c1$output_files())
print(stanfit1)
## Inference for Stan model: model1-202106190132-1-6686ed.
## 4 chains, each with iter=21000; warmup=1000; thin=1;
## post-warmup draws per chain=20000, total post-warmup draws=80000.
##
## mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
## delta 0.27 0.00 0.10 0.07 0.20 0.27 0.34 0.47 62133 1
## sigma 8.15 0.00 0.58 7.11 7.75 8.12 8.53 9.39 58529 1
## g 3.49 0.81 217.23 0.08 0.21 0.42 1.00 11.79 71142 1
## mean_delta 0.27 0.00 0.02 0.23 0.26 0.27 0.29 0.31 62414 1
## variance_delta 0.01 0.00 0.00 0.01 0.01 0.01 0.01 0.01 75686 1
## BF_01 0.23 0.00 0.13 0.06 0.13 0.20 0.29 0.54 54358 1
## logPostDensDelta -2.44 0.00 0.56 -3.62 -2.80 -2.41 -2.05 -1.42 61613 1
## logPriorDensDelta -0.80 0.00 0.00 -0.80 -0.80 -0.80 -0.80 -0.80 2 1
## lp__ -379.97 0.01 1.28 -383.31 -380.56 -379.64 -379.03 -378.50 32010 1
##
## Samples were drawn using NUTS(diag_e) at Sat Jun 19 01:32:05 2021.
## For each parameter, n_eff is a crude measure of effective sample size,
## and Rhat is the potential scale reduction factor on split chains (at
## convergence, Rhat=1).
ms1 <- as.matrix(stanfit1)
res1 <- ms1 %>% as.data.frame() %>% select(starts_with("BF")) %>%
summarise_all(list(mean = mean)) %>% summarise_all(list(round),digits=8) %>% pivot_longer(everything())
cat(sprintf("Bayesfactor is\n\tBF_01:%.8f\tBF_10:%.8f",res1$value, 1 / res1$value))
## Bayesfactor is
## BF_01:0.22509123 BF_10:4.44264310
Rhatで収束を確認。結果は
$$
\begin{cases}
BF_{01} \fallingdotseq 0.225 \\
BF_{10} \fallingdotseq 4.443
\end{cases}
$$
となりました。Kass and Raftery(1995)の評価基準では、$H_0$に対する反証の強さは十分であると判断できます。つまり、$\delta = 0$を棄却し$\delta \neq 0$を採択し、対策後の事故件数は対策前から変化したと判断してよさそうです。
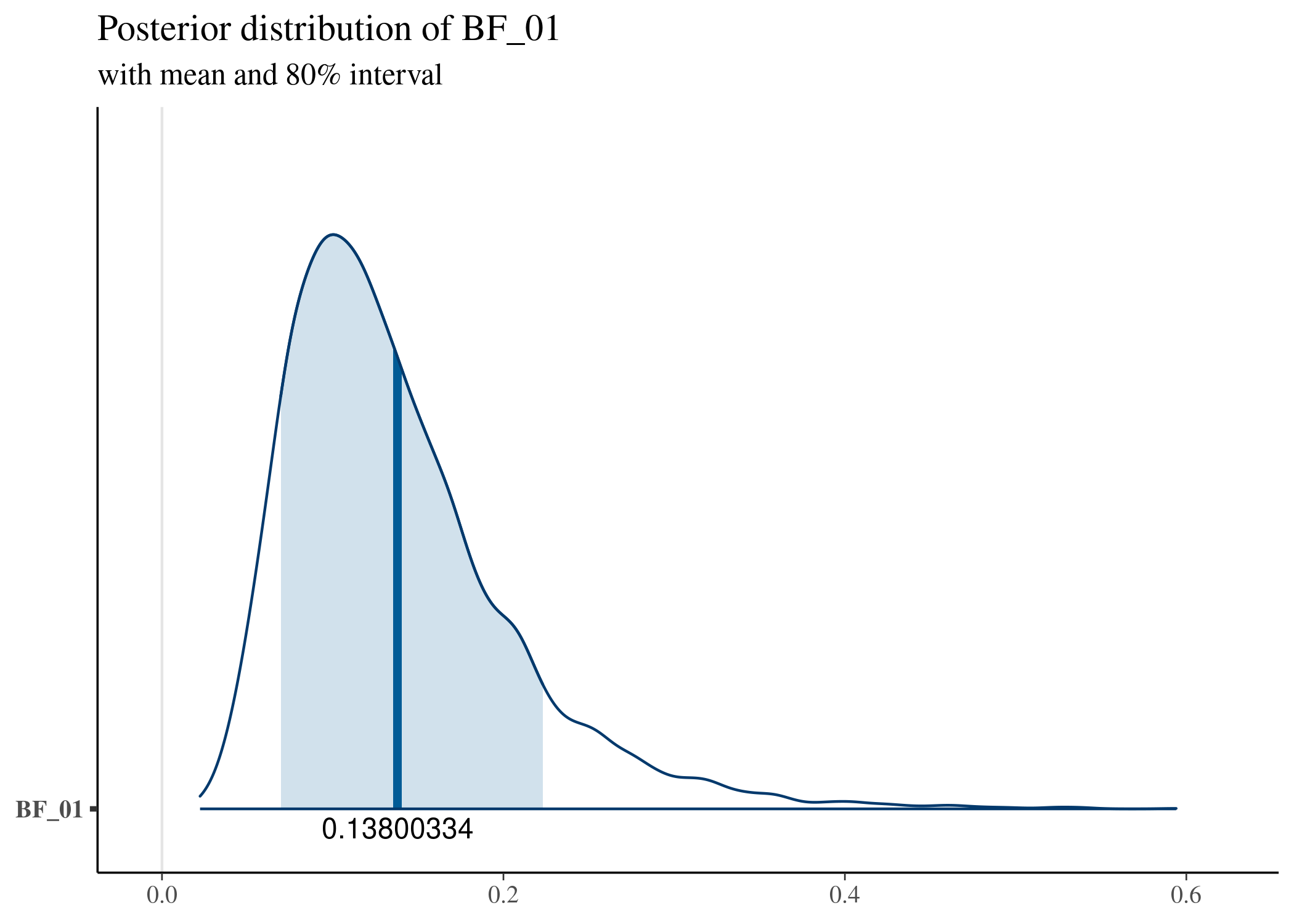
$BF_{01}$の分布も確認しておきましょう。

plot_title <- ggtitle("Posterior distribution of BF_01",
"with mean and 80% interval")
p <- mcmc_areas(ms1,
pars = c("BF_01"),
prob = 0.8, point_est = c("mean")) +
geom_text(data=res1[2], aes(x=value, y="BF_01", label=value), nudge_y =-0.03) + plot_title
一応、以上の結果がまともなのかどうか、BayesFactorパッケージで確認します。
library(BayesFactor)
bf <- ttestBF(x=d$pre, y=d$pro, paired=T)
bf
## Bayes factor analysis
## --------------
## [1] Alt., r=0.707 : 4.297253 ±0%
##
## Against denominator:
## Null, mu = 0
## ---
## Bayes factor type: BFoneSample, JZS
1 / bf
## Bayes factor analysis
## --------------
## [1] Null, mu=0 : 0.2327068 ±0%
##
## Against denominator:
## Alternative, r = 0.707106781186548, mu =/= 0
## ---
## Bayes factor type: BFoneSample, JZS
BayesFactor::ttestBF()による結果は、
$$
\begin{cases}
BF_{01} \fallingdotseq 0.233 \\
BF_{10} \fallingdotseq 4.297
\end{cases}
$$
でした。概ね俺の実装による結果と整合してそうです。
片側検定
間髪を入れず片側検定に移ります。モデル構成は両側検定のときから変わらないので、先ほど得たMCMCサンプルをこねくり回します。 $H_{1PO}$、$H_{1NO}$に対応するモデルをそれぞれ$M_{1PO}$、$M_{1NO}$とおくと、
$$
\begin{cases}
p(\delta = 0 | M_{1NO}) = p(\delta = 0 | M_{1PO}) = \cfrac{2}{\pi r} \\
p(\delta=0 | \mathcal{D}, M_{1PO}) = \cfrac{p(\delta=0 | \mathcal{D}, M_1)}{\Phi(0 | \mu_{\delta}, \sigma_{\delta})} \eqsim \cfrac{1}{T} \sum_{t=1}^{T} \cfrac{p(\delta=0 | \boldsymbol{\psi}^{(t)},\mathcal{D},M_1)}{\Phi(0 | \mu_{\delta}^{(t)}, \sigma_{\delta}^{(t)})} \\
p(\delta=0 | \mathcal{D}, M_{1NO}) = \cfrac{p(\delta=0 | \mathcal{D}, M_1)}{1 - \Phi(0 | \mu_{\delta}, \sigma_{\delta})} \eqsim \cfrac{1}{T} \sum_{t=1}^{T} \cfrac{p(\delta=0 | \boldsymbol{\psi}^{(t)},\mathcal{D},M_1)}{1 - \Phi(0 | \mu_{\delta}^{(t)}, \sigma_{\delta}^{(t)})} \\
\end{cases}
$$
だから、Savage-Dickey法より
$$ BF_{01PO} = \cfrac{p(\delta=0 | \mathcal{D}, M_{1PO})}{p(\delta=0 | M_{1PO})} \eqsim \cfrac{\pi r}{2} \cfrac{1}{T} \sum_{t=1}^{T} \cfrac{p(\delta=0 | \boldsymbol{\psi}^{(t)},\mathcal{D},M_1)}{\Phi(0 | \mu_{\delta}^{(t)}, \sigma_{\delta}^{(t)})} = \cfrac{1}{T} \sum_{t=1}^{T}\cfrac{BF_{01}^{(t)}}{2\Phi(0 | \mu_{\delta}^{(t)}, \sigma_{\delta}^{(t)}) } $$
$$ BF_{01NO} = \cfrac{p(\delta=0 | \mathcal{D}, M_{1NO})}{p(\delta=0 | M_{1NO})} \eqsim \cfrac{\pi r}{2} \cfrac{1}{T} \sum_{t=1}^{T} \cfrac{p(\delta=0 | \boldsymbol{\psi}^{(t)},\mathcal{D},M_1)}{1 - \Phi(0 | \mu_{\delta}^{(t)}, \sigma_{\delta}^{(t)})} = \cfrac{1}{T} \sum_{t=1}^{T}\cfrac{BF_{01}^{(t)}}{2\left(1 - \Phi(0 | \mu_{\delta}^{(t)}, \sigma_{\delta}^{(t)})\right) } $$
です(*´Д`)ハァハァ。
res_ordered <- ms1 %>% data.frame() %>% mutate(BF_01_NO = BF_01 / (2 * (1-pnorm(0, mean=mean_delta, sd=sqrt(variance_delta)))),
BF_01_PO = BF_01 / (2 * pnorm(0, mean=mean_delta, sd=sqrt(variance_delta))),
BF_10_NO = (2 * (1-pnorm(0, mean=mean_delta, sd=sqrt(variance_delta))) / BF_01),
BF_10_PO = (2 * pnorm(0, mean=mean_delta, sd=sqrt(variance_delta)))/ BF_01) %>%
summarise(BF_01_NO = mean(BF_01_NO),
BF_01_PO = mean(BF_01_PO),
BF_10_NO = mean(BF_10_NO),
BF_10_PO = mean(BF_10_PO))
res_ordered
## BF_01_NO BF_01_PO BF_10_NO BF_10_PO
## 1 0.1130584 34.61659 12.16943 0.02898778
# 推定精度の良い(BF<1となる)方を用いる
cat(sprintf("Bayesfactor is\n\tBF_01_NO:%.8f\tBF_10_NO:%.8f\n\tBF_01_PO:%.8f\tBF_10_PO:%.8f",
res_ordered$BF_01_NO, 1 / res_ordered$BF_01_NO,
1 /res_ordered$BF_10_PO, res_ordered$BF_10_PO))
## Bayesfactor is
## BF_01_NO:0.11305844 BF_10_NO:8.84498327
## BF_01_PO:34.49729577 BF_10_PO:0.02898778
結果は
$$
\begin{cases}
BF_{01PO} \fallingdotseq 34.497 \\
BF_{10PO} \fallingdotseq 0.029 \\
BF_{01NO} \fallingdotseq 0.113 \\
BF_{10NO} \fallingdotseq 8.845 \\
\end{cases}
$$
でした。Kass and Raftery(1995)の評価基準では、$H_{1PO}$に反する証拠は強く、$H_{0NO}$に反する証拠は十分にあると判断できます。つまり、$\delta \leq 0$と$\delta=0$の比較では$\delta=0$が採択されることから、事故件数平均値は対策後増加していないと判断され、さらに$\delta \geq 0$と$\delta=0$の比較では$\delta \geq 0$が採択されることから、やはり対策後の事故件数の平均値は減少したのだと判断されます。
BayesFactorパッケージとの整合を確認します。
# bayesfactorパッケージでordered restrictionのベイズファクターを計算
bf <- ttestBF(x=d$pre, y=d$pro, nullInterval = c(0,Inf) ,paired=T)
bf
## Bayes factor analysis
## --------------
## [1] Alt., r=0.707 0<d<Inf : 8.564529 ±0%
## [2] Alt., r=0.707 !(0<d<Inf) : 0.02997665 ±0.01%
##
## Against denominator:
## Null, mu = 0
## ---
## Bayes factor type: BFoneSample, JZS
1/bf
## denominator
## numerator Alt., r=0.707 0<d<Inf Alt., r=0.707 !(0<d<Inf)
## Null, mu=0 0.1167606 33.35929
BayesFactor::ttestBF()による結果は、
$$
\begin{cases}
BF_{01PO} \fallingdotseq 33.359 \\
BF_{10PO} \fallingdotseq 0.030 \\
BF_{01NO} \fallingdotseq 0.117 \\
BF_{10NO} \fallingdotseq 8.565 \\
\end{cases}
$$
でした。やはり俺の実装による結果と整合しているな(;´Д`)スッ、スバラスィ …ハァハァ。
2つの範囲仮説を検証
範囲仮説については理論編でもこれまでも説明していませんでした。Richard D. Morey氏らの論文で説明されているもので、帰無仮説が$\delta$のパラメータ空間上の1点ではなく、一定の範囲をもつ場合になります。微小な平均値の差は効果が無いに等しいものとして扱いたいときに有効な方法です。
範囲仮説同士のベイズファクターは、両仮説に対応するモデル$M_0$、$M_1$を包含したモデル(encompassing model)$M_E$を設定すれば、 $$ BF_{01} = \cfrac{p( \mathcal{D} | \delta \in A, M_E )}{p(\mathcal{D} | \delta \notin A, M_E )} = \left. \cfrac{p( \delta \in A | \mathcal{D},M_E)}{p(\delta \notin A| \mathcal{D}, M_E)} \middle/ \cfrac{p( \delta \in A | M_E)}{p(\delta \notin A | M_E)} \right. $$
と計算できます。
このうち、事前分布の範囲確率$p( \delta \notin A| \mathcal{D}, M_E)$、$p(\delta \in A| \mathcal{D}, M_E)$はまがうことなきClosed formで計算できるとして、引っかかるのが尤度$p(\delta \in A | \mathcal{D}, M_E)$、$p(\delta \notin A | \mathcal{D}, M_E)$です。要は$\delta$の累積分布関数を$\Phi(\delta)$とおいて、
$$
\begin{cases}
p(\delta \in A | \mathcal{D}, M_E) \eqsim \cfrac{1}{T} \sum_{t=1}^{T} \left( \Phi(\delta_u | \mu_{\delta}^{(t)}, \sigma_{\delta}^{(t)}) - \Phi(\delta_l | \mu_{\delta}^{(t)}, \sigma_{\delta}^{(t)}) \right) \\
p(\delta \notin A | \mathcal{D}, M_E) \eqsim 1 - p(\delta \in A | \mathcal{D}, M_E)
\end{cases}
$$
を計算すればいいのですが、$\delta$の密度関数の平均$\mu_{\delta}^{(t)}$、分散$\sigma_{\delta}^{(t)}$を精度よく推定してやる工夫が必要と考えられます。 しかしこれも理論編をしっかり抑えていれば、理論編$(18)$式、$(20)$式を用いてやればよいと分かるはずです(*´Д`)ハァハァ。
これもモデル構成は両側検定のときから変わらないので、両側検定のMCMCサンプルをこねくり回します。2つの仮説の境界は$\delta_l = -2 / \sigma$、 $\delta_u < -2 / \sigma$、つまり事故発生件数$\pm2$程度の微小な増減は無視したいという志向で仮説を設定します。
# Area null
upper_effect <- 2
lower_effect <- -2
r <- stan_data$r
res_Area <- ms1 %>% data.frame() %>%
mutate(upper_delta = upper_effect / sigma, lower_delta = lower_effect / sigma,postAreadelta = pnorm(upper_delta, mean=mean_delta, sd=sqrt(variance_delta)) -pnorm(lower_delta, mean=mean_delta, sd=sqrt(variance_delta)),
priorAreadelta = pcauchy(upper_delta, 0, r) - pcauchy(lower_delta, 0, r)) %>%
mutate(BF_10_Area = (1-postAreadelta) / postAreadelta / ((1-priorAreadelta) / priorAreadelta)) %>%
summarise(BF_10_Area = mean(BF_10_Area)) %>% mutate(BF_01_Area = 1 / BF_10_Area)
## res_Area <- ms1 %>% data.frame() %>%
## mutate(upper_delta = upper_effect / sigma, lower_delta = lower_effect / sigma,postAreadelta = pnorm(upper_delta, mean=mean_delta, sd=sqrt(variance_delta)) -pnorm(lower_delta, mean=mean_delta, sd=sqrt(variance_delta)),
## priorAreadelta = pcauchy(upper_delta, 0, r) - pcauchy(lower_delta, 0, r)) %>%
## mutate(BF_01_Area = postAreadelta/(1-postAreadelta) / (priorAreadelta/(1-priorAreadelta))) %>%
## summarise(BF_01_Area = mean(BF_01_Area)) %>% mutate(BF_10_Area = 1 / BF_01_Area)
res_Area
## BF_10_Area BF_01_Area
## 1 0.4152557 2.408155
結果は、
$$
\begin{cases}
BF_{01Area} \fallingdotseq 2.408 \\
BF_{10Area} \fallingdotseq 0.415 \\
\end{cases}
$$
となりました。$H_{0Area}$の方が支持されるものの、Kass and Raftery(1995)の評価基準では、$H_{1Area}$に反する証拠は十分でないと判断されます。つまり、$\pm2$以上の事故件数の増減はなかったといえそうだが、その証拠は十分ではない、ということです。
BayesFactorパッケージとの整合を確認します。
X <- scale(d$pre - d$pro)
bf <- ttestBF(x=d$pre, y=d$pro, nullInterval = c(-2,2)/attr(X, "scaled:scale") ,paired=T)
bf[1]/bf[2]
## Bayes factor analysis
## --------------
## [1] Alt., r=0.707 -0.245057417614946<d<0.245057417614946 : 2.472662 ±0%
##
## Against denominator:
## Alternative, r = 0.707106781186548, mu =/= 0 !(-0.245057417614946<d<0.245057417614946)
## ---
## Bayes factor type: BFoneSample, JZS
bf[2]/bf[1]
## Bayes factor analysis
## --------------
## [1] Alt., r=0.707 !(-0.245057417614946<d<0.245057417614946) : 0.4044224 ±0%
##
## Against denominator:
## Alternative, r = 0.707106781186548, mu =/= 0 -0.245057417614946<d<0.245057417614946
## ---
## Bayes factor type: BFoneSample, JZS
BayesFactor::ttestBF()による結果は、
$$
\begin{cases}
BF_{01Area} \fallingdotseq 2.473 \\
BF_{10Area} \fallingdotseq 0.404 \\
\end{cases}
$$
やはり俺の実装はうまくいってそうだ(;´Д`)スッ、スバラスィ …ハァハァ。
対応のない検定を実践
対応のない検定は、尤度が異なる点を除き対応のある検定と同じです。
サンプルデータの可視化
データは対応のある検定のときと同じものを用います。命名と実際の意味が少し異なっていて分かりづらいですが、d$preは対策A未実施の交差点における事故発生件数、d$proは対策A実施済みの交差点における事故発生件数とします。
視覚化はこんな感じです。
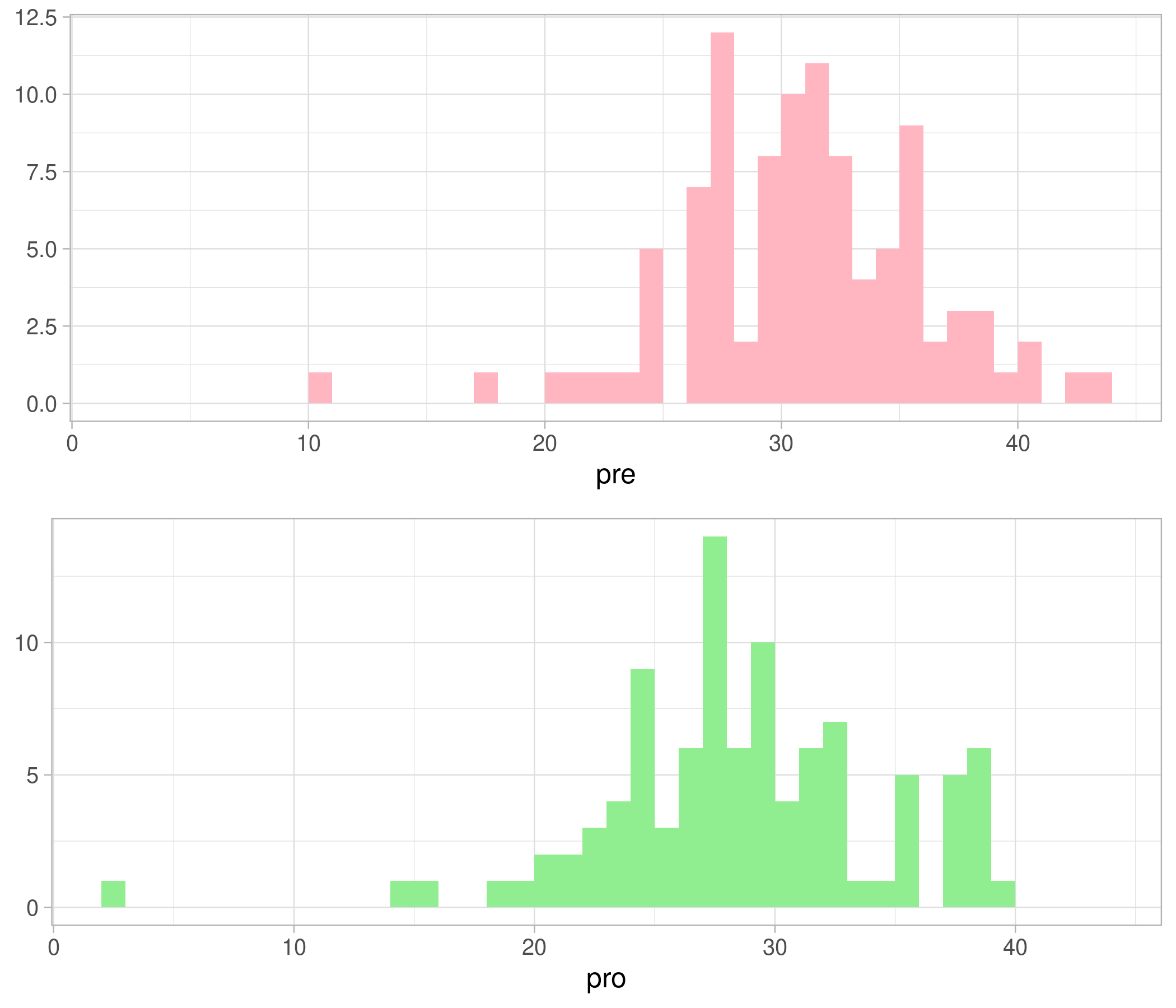
可視化コードはこちら。
p1 <- ggplot(data.frame(X = d$pre), aes(x=X)) + theme_light(base_size=12) + geom_histogram(breaks=seq(min(c(d$pre,d$pro)), max(c(d$pre,d$pro)), 1),
fill="#ffb6c1") + xlab("pre") + ylab(NULL)
p2 <- ggplot(data.frame(X = d$pro), aes(x=X)) + theme_light(base_size=12) + geom_histogram(breaks=seq(min(c(d$pre,d$pro)), max(c(d$pre,d$pro)), 1),
fill="#90ee90") + xlab("pro") + ylab(NULL)
library(gridExtra)
p <- grid.arrange(p1,p2, nrow=2)
両側検定
Stanコードは以下のとおり。
//model2.stan
//Two-sample t-test
data{
int N; //sample size og group1
int M; //sample size of group2
vector[N] D1; //data of group1
vector[M] D2; //data of group2
real<lower=0> r, Jeffreys_alpha, Jeffreys_beta;
//r:scale factor
//Jeffreys_alpha:mean of prior(sigma^2) (sufficiently small values)
//Jeffreys_beta:variance of prior(sigma^2) (sufficiently small values)
}
parameters{
real delta, mu; //delta:effect size mu:overall mean
real<lower=0> sigma, g;
}
model{
//Likelihood
target += normal_lpdf(D1 | mu - delta * sigma / 2, sigma);
target += normal_lpdf(D2 | mu + delta * sigma / 2, sigma);
//JZS prior
target += normal_lpdf(delta | 0, sqrt(g));
target += inv_gamma_lpdf(g | 0.5 , (r^2)*0.5);
target += gamma_lpdf(sigma^2 | Jeffreys_alpha, Jeffreys_beta);
}
generated quantities{
real mean_delta, variance_delta;
//mean_delta:mean of CMDE(delta)
//variance_delta:variance of CMDE(delta)
real BF_01;
// real BF_10;
real logPostDensDelta, logPriorDensDelta;
//logPostDensDelta:p(delta=0 | prior)
//logPostDensDelta:p(delta=0 | posterior)
mean_delta = 2 * g * (sum(D2) - sum(D1) + (N - M) * mu ) / ((4 + ( N + M ) * g ) * sigma);
variance_delta = 4 * g / (4 + (N + M) * g);
logPostDensDelta = -0.5 * log(pi() * variance_delta * 2) - 0.5 * mean_delta^2 / variance_delta;
logPriorDensDelta = -log(pi() * r);
BF_01 = exp(logPostDensDelta - logPriorDensDelta);
//BF_10 = exp(logPriorDensDelta - logPostDensDelta);
}
これを走らせるRコードはこちら。
stan_data <- list(D1=d$pro, D2=d$pre, N = length(d$pro), M = length(d$pre), r =sqrt(2)/2, Jeffreys_alpha=1e-10, Jeffreys_beta=1e-10)
model2_c <- cmdstan_model("/model/model2.stan")
fit_c_area <- model3_c$sample(
data = stan_data,
parallel_chains = 4,
chains = 4,
iter_warmup = 500,
iter_sampling = 2000
)
以降のコードは対応のある場合と基本的に同じなので、結果だけ載せていきますね |ω·`)
## Inference for Stan model: model3-202106202142-1-61dec5.
## 4 chains, each with iter=2500; warmup=500; thin=1;
## post-warmup draws per chain=2000, total post-warmup draws=8000.
##
## mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
## delta 0.39 0.00 0.14 0.12 0.29 0.39 0.48 0.66 8173 1
## mu 30.28 0.00 0.39 29.53 30.02 30.28 30.55 31.07 7252 1
## sigma 5.60 0.00 0.28 5.09 5.40 5.58 5.78 6.17 7184 1
## g 3.59 0.93 67.27 0.09 0.23 0.47 1.13 13.19 5182 1
## mean_delta 0.39 0.00 0.03 0.32 0.37 0.39 0.41 0.44 7823 1
## variance_delta 0.02 0.00 0.00 0.02 0.02 0.02 0.02 0.02 8608 1
## BF_01 0.14 0.00 0.07 0.05 0.09 0.12 0.17 0.31 6952 1
## logPostDensDelta -2.88 0.01 0.46 -3.79 -3.19 -2.89 -2.58 -1.97 7593 1
## lp__ -655.90 0.02 1.44 -659.60 -656.61 -655.56 -654.83 -654.11 3423 1
## logPriorDensDelta -0.80 0.00 0.00 -0.80 -0.80 -0.80 -0.80 -0.80 2 1
##
## Samples were drawn using NUTS(diag_e) at Sun Jun 20 21:42:05 2021.
## For each parameter, n_eff is a crude measure of effective sample size,
## and Rhat is the potential scale reduction factor on split chains (at
## convergence, Rhat=1).
## Bayesfactor is
## BF_01:0.13800334 BF_10:7.24620143
結果は
$$
\begin{cases}
BF_{01} \fallingdotseq 0.138 \\
BF_{10} \fallingdotseq 7.246 \\
\end{cases}
$$
です。よって$H_1$を採択し、2グループ間の事故件数には差があると判断されます。
BayesFactorパッケージの場合は、
bf <- ttestBF(x=d$pre, y=d$pro, paired=F)
bf
## Bayes factor analysis
## --------------
## [1] Alt., r=0.707 : 7.149843 ±0%
##
## Against denominator:
## Null, mu1-mu2 = 0
## ---
## Bayes factor type: BFindepSample, JZS
1 / bf
## Bayes factor analysis
## --------------
## [1] Null, mu1-mu2=0 : 0.1398632 ±0%
##
## Against denominator:
## Alternative, r = 0.707106781186548, mu =/= 0
## ---
## Bayes factor type: BFindepSample, JZS
$$
\begin{cases}
BF_{01} \fallingdotseq 0.140 \\
BF_{10} \fallingdotseq 7.150 \\
\end{cases}
$$
ほぼ一致Σ(゚Д゚)スゲェ!
片側検定
## Bayesfactor is
## BF_01_NO:0.06924356 BF_10_NO:14.44177639
## BF_01_PO:25.05332284 BF_10_PO:0.03991487
俺の実装による結果は
$$
\begin{cases}
BF_{01PO} \fallingdotseq 25.053 \\
BF_{10PO} \fallingdotseq 0.040 \\
BF_{01NO} \fallingdotseq 0.069 \\
BF_{10NO} \fallingdotseq 14.442 \\
\end{cases}
$$
今回の実装で$\delta$は「未対策の交差点における事故件数の平均値」-「対策済みの交差点における事故件数の平均値」の値です。まず$H_{0PO}$が強く採択されることから、「対策済み」グループのほうが「未対策」グループよりも事故件数の平均値が多い、ということはないと判断できます。さらに、$H_{1NO}$が採択されることから、「未対策」グループのほうが「対策済み」グループよりも事故件数の平均値が多いと言えると判断できます。
bf <- ttestBF(x=d$pre, y=d$pro, nullInterval = c(0,Inf) ,paired=F)
bf
## Bayes factor analysis
## --------------
## [1] Alt., r=0.707 0<d<Inf : 14.25912 ±0%
## [2] Alt., r=0.707 !(0<d<Inf) : 0.04056425 ±0.17%
##
## Against denominator:
## Null, mu1-mu2 = 0
## ---
## Bayes factor type: BFindepSample, JZS
1/bf
## denominator
## numerator Alt., r=0.707 0<d<Inf Alt., r=0.707 !(0<d<Inf)
## Null, mu1-mu2=0 0.07013055 24.65225
パッケージによる結果は
$$
\begin{cases}
BF_{01PO} \fallingdotseq 24.652 \\
BF_{10PO} \fallingdotseq 0.041 \\
BF_{01NO} \fallingdotseq 0.070 \\
BF_{10NO} \fallingdotseq 14.259 \\
\end{cases}
$$
ほぼ一致…(;´Д`)スッ、スバラスィ …ハァハァ
2つの範囲仮説を検証
対応のある場合と同様、2つの仮説の境界は$\delta_l = -2 / \sigma$、 $\delta_u < -2 / \sigma$とします。
BF_10_Area BF_01_Area
1 0.5996078 1.667757
俺の実装による結果は、
$$
\begin{cases}
BF_{01Area} \fallingdotseq 1.668 \\
BF_{10Area} \fallingdotseq 0.600 \\
\end{cases}
$$
よって、$H_{0Area}$の方がデータの説明力は高いものの、決定的でないことが分かります。つまりグループ間に$\pm2$以上の事故件数の平均値の差はないといえそうだが、その証拠は十分ではない、ということです。
X <- scale(c(d$pre,d$pro))
attr(X, "scaled:scale")
bf <- ttestBF(x=d$pre, y=d$pro, nullInterval = c(-2,2)/attr(X, "scaled:scale") ,paired=F)
bf[1]/bf[2]
## Bayes factor analysis
## --------------
## [1] Alt., r=0.707 -0.351290094235453<d<0.351290094235453 : 1.638839 ±0%
##
## Against denominator:
## Alternative, r = 0.707106781186548, mu =/= 0 !(-0.351290094235453<d<0.351290094235453)
## ---
## Bayes factor type: BFindepSample, JZS
bf[2]/bf[1]
## Bayes factor analysis
## --------------
## [1] Alt., r=0.707 !(-0.351290094235453<d<0.351290094235453) : 0.6101882 ±0%
##
## Against denominator:
## Alternative, r = 0.707106781186548, mu =/= 0 -0.351290094235453<d<0.351290094235453
## ---
パッケージによる結果は、
$$
\begin{cases}
BF_{01Area} \fallingdotseq 1.639 \\
BF_{10Area} \fallingdotseq 0.610 \\
\end{cases}
$$
最後の検定結果もほぼ同じ、無事有終の美を飾ることができました。
