2021.02.14 00:00

ベイズファクター

本記事ではベイジアンモデルに対するモデル評価の指標であるベイズファクターについて理論を整理します。

まず、情報量について、エントロピーを踏まえながら理解します。次に、情報量から自由エネルギーを定義し、これが周辺尤度とも深く関連することを理解します。以上の理論的な準備を踏まえ、ベイズファクターを定義します。

後半では、具体的な確率分布を用いた計算を例に自由エネルギーやベイズファクターを計算し、それらを用いたモデル評価の性質をシミュレーションで確認します。

参考にした本はこちらです。モデル評価の指標について分かりやすい説明が並んでいます。この本によれば、モデル評価の指標は自由エネルギーに着目したもの（BIC、WBIC、ベイズファクター）と、汎化誤差に着目したもの（AIC、WAIC）に二分されるようですが、本記事ではそのうち前者の方の、ベイズファクターのみに着目して考えます。

情報量

確率がからむある試行について考えたとき、その試行の結果得られた事象が持っている情報の多さはどのくらいなのか？

事象のもつ情報の多さ、すなわち情報量を定量的に表現するための関数$f$の条件について考えます。

連続型の確率変数$X$及びその実現値$x$について、情報量は$P(x)$に依存すると考えられることから、まず関数$f$は$P(x)$を変数にとることとします。

次に、情報量をあらわす$f(P(x))$について望ましい性質として、以下が考えられます。

$$ P(x_i) \leq P(x_j) \Rightarrow f(P(x_i)) \geq f(P(x_j)) \tag{1} $$ $$ f(P(x_i)P(x_j)) = f(P(x_i))f(P(x_j)) \tag{2} $$ $$ f(P(x_i)=1) = 0 \tag{3} $$

$(1)$式は、事象が起きる確率が低い程、その事象が持つ驚きの強さ（情報量）が大きくなるような条件です。
$(2)$式は、2つの事象を1回の試行で同時に得るようなときと、それらの事象を2回の試行で一つひとつ得るようなときの情報量が同じになることを意味する条件です。
$(3)$式は、ある事象が起きる確率が1のとき、情報量が0であることを意味する条件です。

これらの条件を満たす関数として、以下の情報量が導出されます。

◆情報量 連続型の確率変数$X$から実現値$x$が得られたときの情報量は、以下で定義される。 $$ I(X = x) = -\log{P(X = x)}　\tag{4} $$


◆情報量の証明 $x ∈ \mathbb{R}$について微分可能な関数$f(x)$について、条件$(2)$より、 $$ f(x(1 + \delta)) = f(x + x\delta) = f(x) + f(1 + \delta) $$ 二つ目の等号より、 $$ \cfrac{f(x + x\delta) - f(x)}{x\delta} = \cfrac{f(1 + \delta)}{x\delta} $$ 左辺は導関数の定義であるから、 $$ f^{'}(x) = K\cfrac{1}{x} $$ ただし、$K = \cfrac{f(1 + \delta)}{\delta}$。 上式を積分して、 $$ f(x) = K\log{x} + C $$ ここで、条件(1)より、$K$は任意の負の実数である。 また条件$(3)$より、$C=1$。 よって、$K=-1$とすることにより$(4)$式が導かれる。

エントロピー

エントロピーは、前節で定義した情報量の期待値です。そのため平均情報量とも呼ばれます。

◆エントロピー

$A ∈ \mathbb{R}$上で定義された確率密度関数$f(x)$をもつ連続型の確率変数$x$のエントロピー$H(X)$を情報量の期待値として下記のとおり定義する。 $$ H(X) = - \int_{A} f(x)\log{f(x)}dx \tag{5} $$

同様に、確率質量関数$g(x)$をもつ離散型の確率変数$X$のエントロピー$H(X)$を以下の通り定義する。 $$ H(X) = \sum_{i=1}^{n}-g(x_i)\log{g(x_i)} \tag{6} $$

エントロピーは、情報量の期待値ですから、確率分布の分散が大きいような、不確実性の大きな条件下でより大きな値を取ることが想定されます。これをガンマ分布を例に確認してみましょう。

shapeパラメータ$a$、rateパラメータ$b$をもつガンマ分布

$$ \mathrm{Gamma}(\lambda | \alpha, \beta) = \cfrac{\beta^{\alpha}}{\Gamma(\alpha)}\lambda^{\alpha -1} e^{-\beta x} \tag{7} $$

の形状は、下図ようになっています。ここで、$\lambda ∈ \mathbb{R}^+, \alpha∈ \mathbb{R}^+, \beta ∈ \mathbb{R}^+$です。

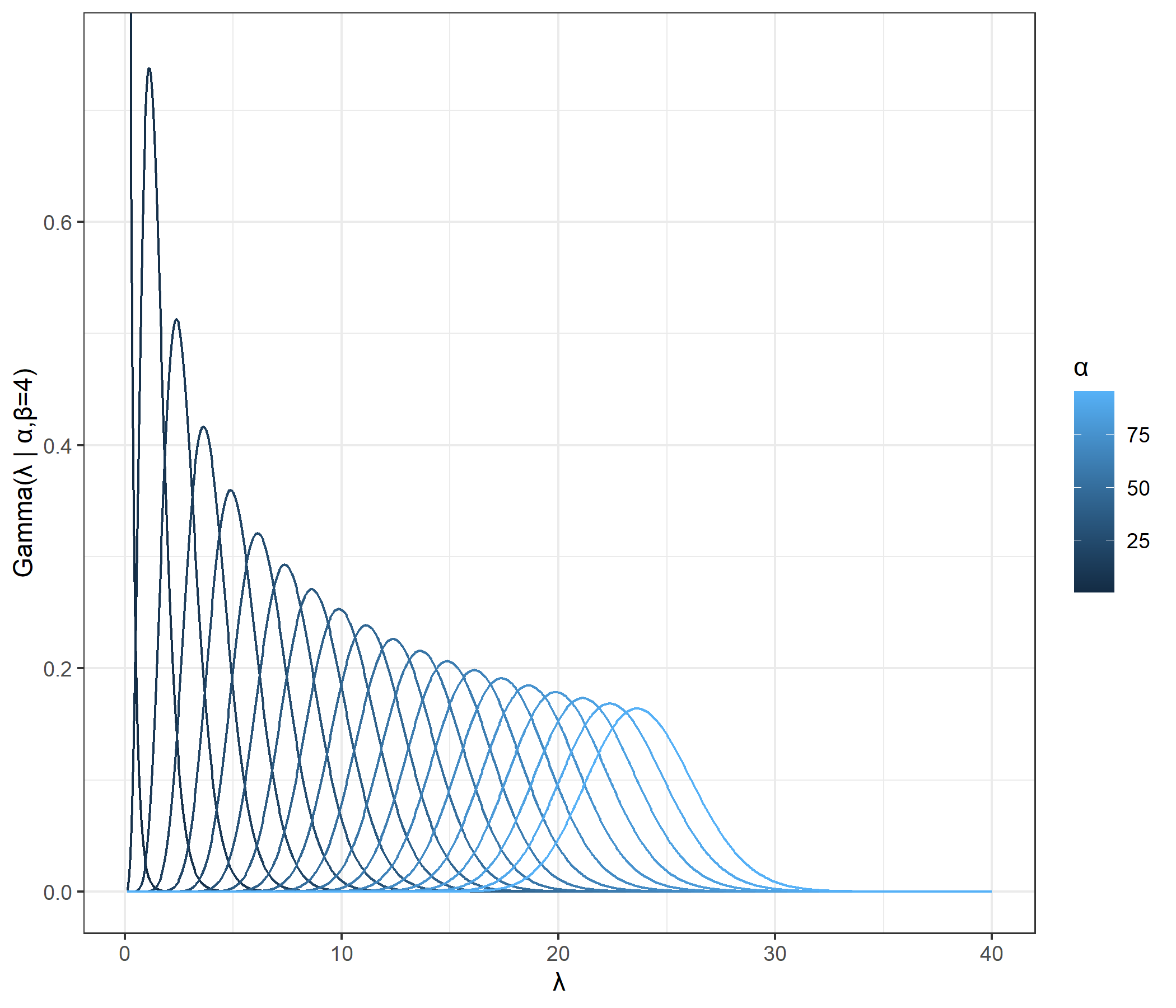
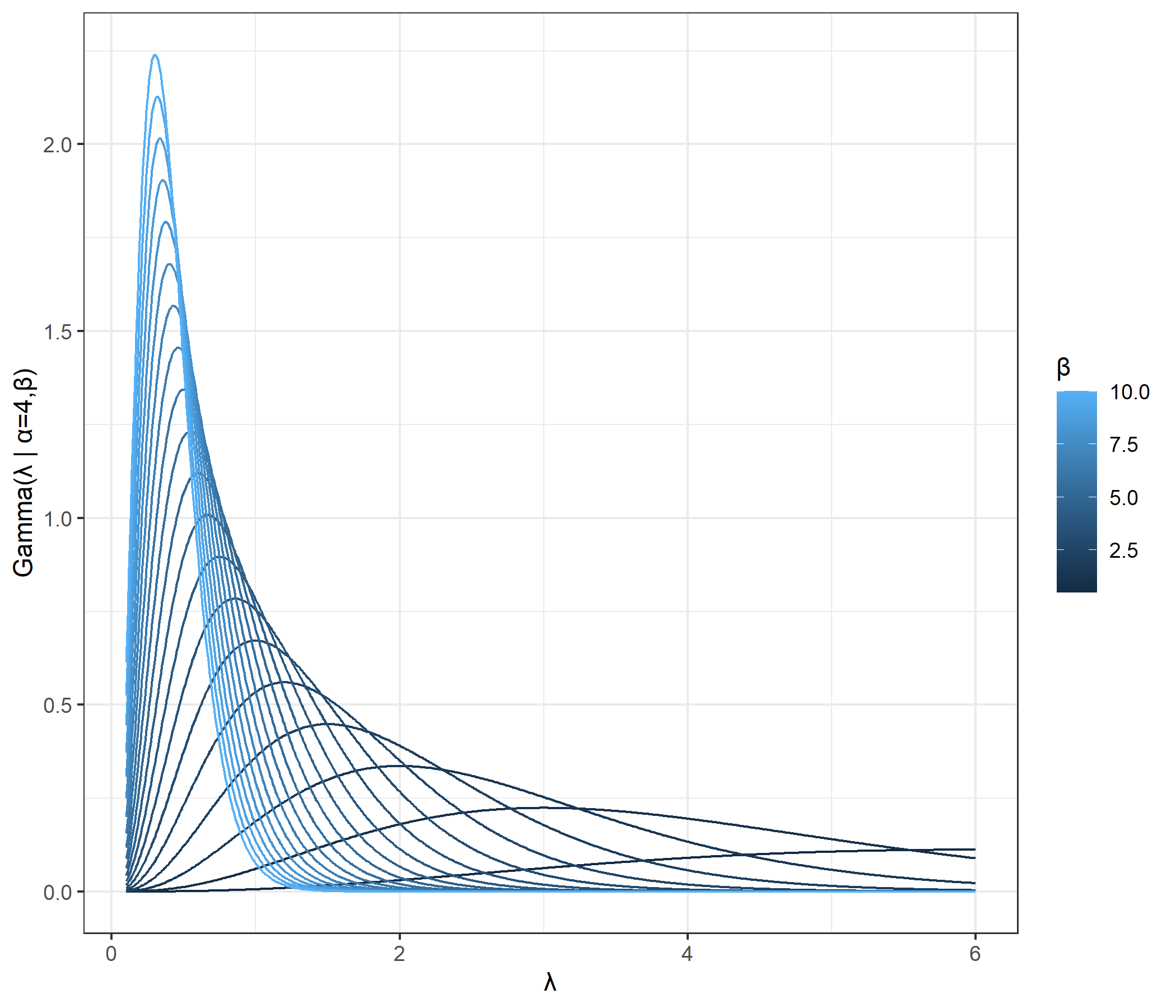
1つ目の図はrateパラメータ固定、shapeパラメータを変化させたときのガンマ分布の形状を示しています。また2つ目の図はshapeパラメータ固定、rateパラメータを変化させたときのガンマ分布の形状を示しています。

これらの図から、shapeパラメータが大きくなるほどまたrateパラメータが小さくなるほど分散は大きくなりそうだと確認できます。実際、以前の記事で確認した通り、ガンマ分布の分散は$\cfrac{\alpha}{\beta^2}$です。

では、同様に片方のパラメータを固定したままもう片方のパラメータを変化させたとき、エントロピーはどのように変化するでしょうか。

それを確認するため、まずガンマ分布のパラメータを変数としてエントロピーを計算します。


◆ガンマ分布のエントロピー shapeパラメータ$\alpha$、rateパラメータ$\beta$のガンマ分布に従う確率変数$\lambda$のエントロピーは、 $$ \begin{split} H(\lambda) &= \mathbb{E}\left[-\log{\lambda}\right] \\\\ &= - \mathbb{E}\left[\alpha\log{\beta} - \log{\Gamma(\alpha)} + (\alpha - 1) \log{\lambda} -\beta\lambda\right] \\\\ &= -\alpha\log{\beta} + \log{\Gamma(\alpha)} + (1-\alpha)\mathbb{E}\left[\log\lambda\right] + \beta\mathbb{E}\left[\lambda\right] \end{split} $$ ここで、$\mathbb{E}\left[\lambda\right] = \cfrac{\alpha}{\beta}$、$\mathbb{E}\left[\log{\lambda}\right] = \psi(\alpha) - \log{\beta}$を用いて、 $$ \begin{split} H(\lambda) &= -\alpha\log{\beta} + \log{\Gamma(\alpha)} + (1-\alpha)(\psi(\alpha) - \log{\beta}) + \beta\left(\cfrac{\alpha}{\beta}\right) \\\\ &= \log{\Gamma(\alpha)} + (1 - \alpha){\psi(\alpha)} - \log{\beta} + \alpha \end{split} $$ ただし、$\psi(x)$はディガンマ関数であり、ガンマ関数を対数微分したもの。

これを用いてガンマ分布のエントロピーを図示したものが、以下になります。

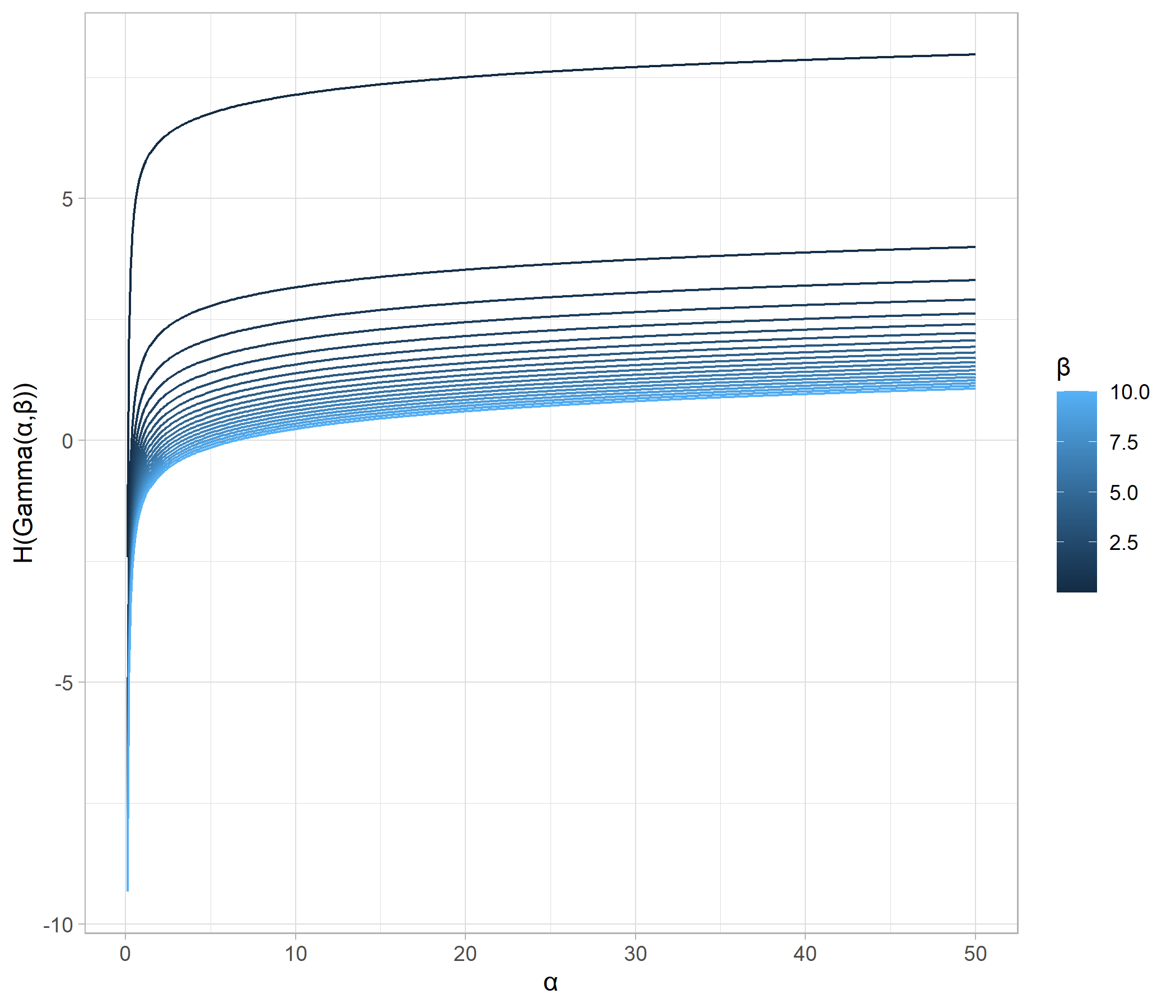
一つ目の図から、ガンマ分布のエントロピーは、shapeパラメータが大きく、すなわち、分散が大きくなるにつれてエントロピーが増大していることが確認できます。
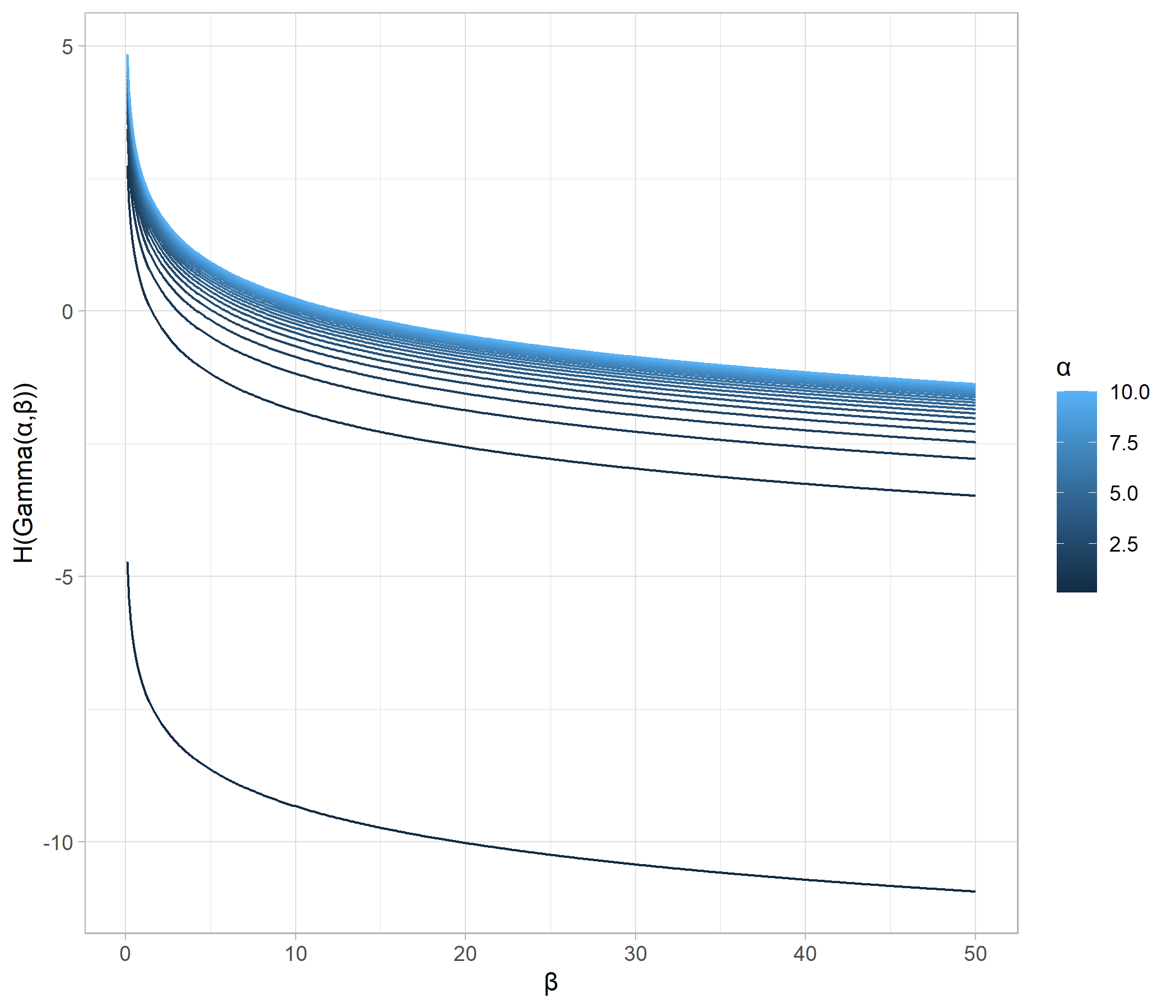
一方、二つ目の図からは、rateパラメータが小さく、すなわち分散が大きくなるにつれてエントロピーが増大していることが確認できます。

以上、分布のばらつきが大きくなるほどエントロピーが大きくなる例を確認しました。エントロピーを通して、情報量が何をはかろうとしているのかイメージしてもらえるかなと思います。

ベイズ自由エネルギー

(逆温度$\beta = -1$の)ベイズ自由エネルギーは、はじめに述べた情報量について、複数の確率変数$X^n = (X_1, X_2,\ldots,X_n)$の同時確率分布の場合の拡張について考え、さらにパラメータの事前分布を想定し、パラメータを周辺化消去したものになります。

◆ベイズ自由エネルギー 確率変数$X^n=(X_1, X_2,\ldots,X_n)$とそれらの同時確率分布$f(x^n)$が与えられたとき、ベイズ自由エネルギー$F_n$は以下のとおり定義される。 $$ F_n = -logf(x^n) = -\log\int_S f(x^n | \theta)\varphi(\theta) d\theta \tag{8} $$ ここで$\theta$は$S ∈ \mathbb{R}$で定義されるパラメータ、$\varphi(\theta)$はパラメータの事前分布、$x^n = (x_1, x_2, \ldots, x_n)$は$X^n$の実現値である。

特に、$X^n$が独立同分布($\mathrm{i.i.d}$)であるとき、その確率関数を$g(x)$とすると、$(8)$式は

$$ F_n = -\log \int \prod_{i=1}^{n}g(x_i | \theta)\varphi(\theta)d\theta \tag{9} $$

となります。

これまで見てきた内容を踏まえると、ベイズ自由エネルギーは、確率変数の実現値（複数）がどれくらい驚きが大きい値かを示す指標であることから、その値が小さいほど、想定したモデルがデータをうまく説明できることを意味していると理解できます。

周辺尤度

実は、$(9)$式は、ベイズに触れたことのある人ならばまず一回は触れたことのある関数とも関連しています。その関数とは、ベイズの定理における正規化定数、すなわち周辺尤度です。

◆事後分布と周辺尤度 標本空間$A ∈ \mathbb{R}$で定義される確率変数$X^n$に関する確率モデル$p(x^n|\theta)$と、$S ∈ \mathbb{R}$で定義されるパラメータ$\theta$の事前分布$\varphi(\theta)$を考えたとき、パラメータの事後分布$p(\theta|x^n)$は下記で定義される。 $$ p(\theta|x^n) = \cfrac{p(x^n|\theta)\varphi(\theta)}{Z_n} \tag{10} $$ $Z_n$は正規化（$\int_S p(\theta|x^n)d\theta = 1$を確約すること）の為の定数であり、周辺尤度という。 $$ Z_n = \int_{S} p(x^n|\theta)\varphi(\theta) d\theta \tag{11} $$

特に、$x^n = (x_1,\ldots,x_n)$が独立同分布（$\mathrm{i.i.d}$）の確率変数からの実現値であるとき、その確率関数を$f(x)$とすると、

$$ p(\theta|x^n) =　\cfrac{\prod_{i=1}^{n} f(x_i|\theta)\varphi(\theta)}{Z_n} \tag{12} $$

$(12)$式が成り立つとき、

$$ Z_n = \int_{S} \prod_{i=1}^{n} f(x_i|\theta)\varphi(\theta) d\theta \tag{13} $$

$Z_n$はパラメータの事後分布の正規化定数であると同時に、確率変数$X^n$の同時確率密度になっています。

$$ \begin{split} \int_A \ldots \int_A Z_n dx_1\ldots dx_n &= \int_A \ldots \int_A \int_S \prod_{i=1}^{n}f(x_i|\theta)\varphi(\theta)d\theta dx_1\ldots dx_n\\\\ &= \int_S \varphi(\theta)d\theta \prod_{i=1}^{n}\int_A f(x_i|\theta)dx_i \\\\ &= 1 \end{split} \tag{13} $$

よって、$Z_n$は実現値$x^n$が得られる同時確率の$\theta$に関する周辺分布($\theta$について周辺化した後の分布)であり、0から1の値をとります。つまり$Z_n$は確率モデル$p(x^n|\theta)$と事前分布$\varphi(\theta)$でデータをうまく説明できているかの指標になります。

$(9)$式と$(12)$式を比較すると、自由エネルギーと周辺尤度の関係が見えてきます。

◆自由エネルギーと周辺尤度の関係 自由エネルギー$F_n$と周辺尤度$Z_n$は以下の関係にある。 $$ F_n = - \log{Z_n} \tag{13} $$

情報量から導かれた自由エネルギー$F_n$は結局のところ$X^n$の同時確率の対数符号反転になることが分かります。

ベイズファクター

ベイズファクターは、2つのモデルを考えたとき、どちらの方が優勢かをはかる指標となります。

◆ベイズファクター 2つの異なるモデル$M_0$、$M_1$を考えたとき、ベイズファクター$BF_{10}$は2つの異なるモデルの周辺尤度の比として定義される。 $$ BF_{10} = \cfrac{p(x^n | M_1)}{p(x^n |M_0)} \tag{14} $$ ここで、$p(x^n | M)$はモデル$M$における周辺尤度である。また$(14)$式を変形することで、自由エネルギーを用いても定義される。 $$ BF_{10} = \exp{(F_{M_0} - F_{M_1})} \tag{15} $$ ここで、$F_M$はモデル$M$における自由エネルギーである。

定義より、$BF_{10}$はモデル$M_0$に比べてモデル$M_1$がどの程度うまくデータを説明できているかを表しており、1より大きい値をとるにつれて$M_1$の方が優勢になっていくことが分かります。

ベイズファクターの評価基準には以下のよく知られたものがあります。

Jeffreys(1961)

$BF_{ij}$ $M_j$に反する証拠の強さ
$1\sim 3.2$ あまりあるとは言えない(Not worth than a bare mention)
$3.2\sim 10$ 十分ある(Substantial)
$10 \sim 100$ 強くある(Strong)
$>100$ 決定的にある(Decisive)

Kass and Raftery(1995)

$BF_{ij}$ $M_j$に反する証拠の強さ
$1\sim 3$ あまりあるとは言えない(Not worth than a bare mention)
$3\sim 20$ 肯定的である(Positive)
$20 \sim 150$ 強くある(Strong)
$>150$ 決定的にある(Very strong)

ベイズファクターを計算する

ベイズファクターの計算は解析的には困難な場合が多いですが、共役事前分布を用いて解析的に計算できる場合もあります。

memo

共役事前分布とは、事前分布と尤度関数を設定したとき、尤度関数のパラメーターの事後分布が事前分布と同じ関数系になるような事前分布のことである。

以下では、$A ∈ \mathbb{R}^+$で定義される独立同分布の$n$個の連続型確率変数$X^n=(X_1,\ldots,X_n)$からの実現値$x^n=(x_1,\ldots,x_n)$をもとに、確率変数$X^n$の分布を推定することを考えます。候補モデルには事後分布を解析的に計算可能なモデルを2つ用意し、どちらのモデルが優勢かをベイズファクターによって判断することを考えます。

モデル1は上述の共役事前分布による事後分布の解析的計算が可能なモデルです。尤度関数には指数分布を設定し、事前分布にはガンマ分布を用いました。

◆モデル１ $$ x_i \sim \mathrm{Exponential}(\gamma) ~~~~ i=1,\ldots,n \tag{16} $$ $$ \gamma \sim \mathrm{Gamma}(\alpha, \beta) \tag{17} $$

◆指数分布の共役事前分布がガンマ分布であることの証明 尤度関数をパラメータ$\gamma$の指数分布 $$ p(x^n | \gamma) = \prod_{i=i}^{n}\left(\gamma\exp(-\gamma x_i)\right) $$ パラメータ$\gamma$の事前分布をshapeパラメータ$\alpha$、rateパラメータ$\beta$のガンマ分布 $$ p(\gamma) = \cfrac{\beta^{\alpha}}{\Gamma(\alpha)}\gamma^{\alpha -1} e^{-\beta \gamma} $$ とするとき、パラメータ$\gamma$の事後分布は、以下の通りガンマ分布である。 $$ \begin{split} p(\gamma | x^n) &\varpropto p(x^n | \gamma)p(\gamma) \\\\ &= \prod_{i=i}^{n}\left(\gamma\exp(-\gamma x_i)\right) \cfrac{\beta^{\alpha}}{\Gamma(\alpha)}\gamma^{\alpha -1} e^{-\beta \gamma} \\\\ &= \gamma ^n \exp(-\gamma \sum_{i=1}^{n}x_i)\cfrac{\beta^{\alpha}}{\Gamma(\alpha)}\gamma^{\alpha -1} e^{-\beta \gamma} \\\\ &= \cfrac{\beta^{\alpha}}{\Gamma(\alpha)} \gamma^{n+\alpha-1}\exp(-(\beta + \sum_{i=1}^{n}x_i)\gamma)\\\\ &\propto \cfrac{\beta^{n + \alpha}}{\Gamma(n + \alpha)} \gamma^{n+\alpha-1}\exp(-(\beta + \sum_{i=1}^{n}x_i)\gamma) \\\\ &= \mathrm{Gamma}(n+\alpha, \beta + \sum_{i=1}^{n}x_i ) \end{split} $$

モデル2は、モデル1と同様、尤度関数に指数分布を設定します。一方、事前分布については設定しないこととします。

◆モデル２ $$ x_i \sim \mathrm{Exponemtial}(\gamma) ~~~~ i=1,\ldots,n \tag{18} $$

ベイズファクターは周辺尤度または自由エネルギーのモデル間比較を行うので、次に上記２モデルの周辺尤度・自由エネルギーを計算します。

モデル1の周辺尤度$p(x^n|M_1)$は、

$$ \begin{split} p(x^n|M_1) &= \int_{0}^{∞}p(x^n | \gamma) \varphi(\gamma) d\gamma \\\\ &= \int_{0}^{∞} \mathrm{Exponential}(x^n | \gamma)\mathrm{Gamma}(\gamma | \alpha, \beta) d\gamma \\\\ &= \int_{0}^{∞} \prod_{i=i}^{n}\left(\gamma\exp(-\gamma x_i)\right) \cfrac{\beta^{\alpha}}{\Gamma(\alpha)}\gamma^{\alpha -1} e^{-\beta \gamma} d\gamma \\\\ &= \cfrac{\beta^{\alpha}}{\Gamma(\alpha)} \int_{0}^{∞} \gamma^{n + \alpha - 1}\exp(-\gamma(\beta +\sum_{i=1}^{n}x_i)) d\gamma \\\\ &= \cfrac{\beta^{\alpha}}{\Gamma(\alpha)} \int_{0}^{∞} \left(\cfrac{\gamma^{'}}{\beta + \sum_{i=1}^{n}x_i }\right)^{(n+\alpha-1)} e^{-\gamma^{'}}\cfrac{1}{\beta + \sum_{i=1}^{n}x_i}d\gamma^{'} ~~~~~\left( (\beta + \sum_{i=1}^{n}x_i)\gamma = \gamma^{'} とした置換積分 \right) \\\\ &= \cfrac{\beta^{\alpha}}{\Gamma(\alpha)(\beta + \sum_{i=1}^{n}x_i)^{n+\alpha}} \int_0^{∞} \gamma^{'(n+\alpha -1)} e^{-\gamma^{'}} d\gamma^{'} \\\\ &= \cfrac{\beta^{\alpha}\Gamma(n+\alpha)}{\Gamma(\alpha)(\beta + \sum_{i=1}^{n}x_i)^{n+\alpha}} ~~~~~(ガンマ関数の定義より) \\\\ &= \cfrac{\beta^{\alpha} n!}{(\beta + \sum_{i=1}^{n}x_i)^{n+\alpha}} ~~~~~(\Gamma(s+1) = s\Gamma(s)より) \end{split} $$

自由エネルギー$F_{M_{1}}$は、

$$ F_{M_{1}} = -log(p(x^n|M_1)) = -\alpha\log\beta - \sum_{i=1}^{n}i + (n + \alpha)\log(\beta + \sum_{i=1}^{n}x_i) \tag{19} $$

同様に、モデル2の周辺尤度$p(x^n|M_2)$と自由エネルギー$F_{M_{2}}$を求めます。

ここで、モデル2についてはパラメーターに事前分布を設定していないので、周辺尤度の計算の際にパラメータで周辺化する必要がありません。よって、

$$ p(x^n|M_2) = \mathrm{Exponential}(x^n | \gamma) = \prod_{i=1}^{n} \gamma \exp(-x_i\gamma) = \gamma^n \exp(-\sum_{i=1}^{n}x_i \gamma) $$ $$ F_{M_2} = -\log(p(x^n | M_2)) = -n\log\gamma + \sum_{i=1}^{n}x_i\gamma \tag{20} $$

では、上記$(19)$、$(20)$式を用いて一つの観測値を例にベイズファクターを計算しましょう。

いま、独立同分布の確率変数の組$X^5$から実現地$x^n = (0.198,0.561,0.572,0.094,0.213)$が得られたとします。このとき、$\alpha=3$、$\beta=1$としたときのモデル1と、$\gamma=3$としたときのモデル2のどちらがよいモデルであるのかを自由エネルギーを用いて比較します。

このときのモデル1の自由エネルギーは、

$$ F_{M_{1}} = -3\log1 - \sum_{i=1}^{5}i + (5 + 3)\log(1 + \sum_{i=1}^{5}x_i) = 2.972677 $$

モデル2の自由エネルギーは、

$$ F_{M_2} = -n\log\gamma + \sum_{i=1}^{n}x_i\gamma = -5\log3 + 3\sum_{i=1}^{5}x_i = 4.914 $$

よって、パラメータに事前分布を設定したモデル1の方がデータをよく説明出来ていることが分かります。また、ベイズファクターを求めると

$$ exp(F_{M_2} - F_{M_1}) = 6.967966 $$

となることから、モデル1の方がやや優勢であると判断することができます。

ベイズファクターの性質を確認する

もうすこし掘り下げて、参考文献を参考に、設定したモデルに対しどのようなデータが得られた時に自由エネルギーの値が大きく（小さく）なるのか見ていきます。ここでは、前節と同じ例を用いて、$X^n$に真の分布を設定し、モデル1($\alpha=3,\beta=1$)、モデル2($\gamma=3$)の比較を行います。

まず、実現値の数を$n=30$とし、真の分布を

$$ X^{30} \sim \mathrm{Exponential}(8) $$

としたとき。実現値の組を1000回発生させ、$F_{M_1}$、$F_{M_2}$をそれぞれ1000回計算し、結果を要約したものが以下になります。

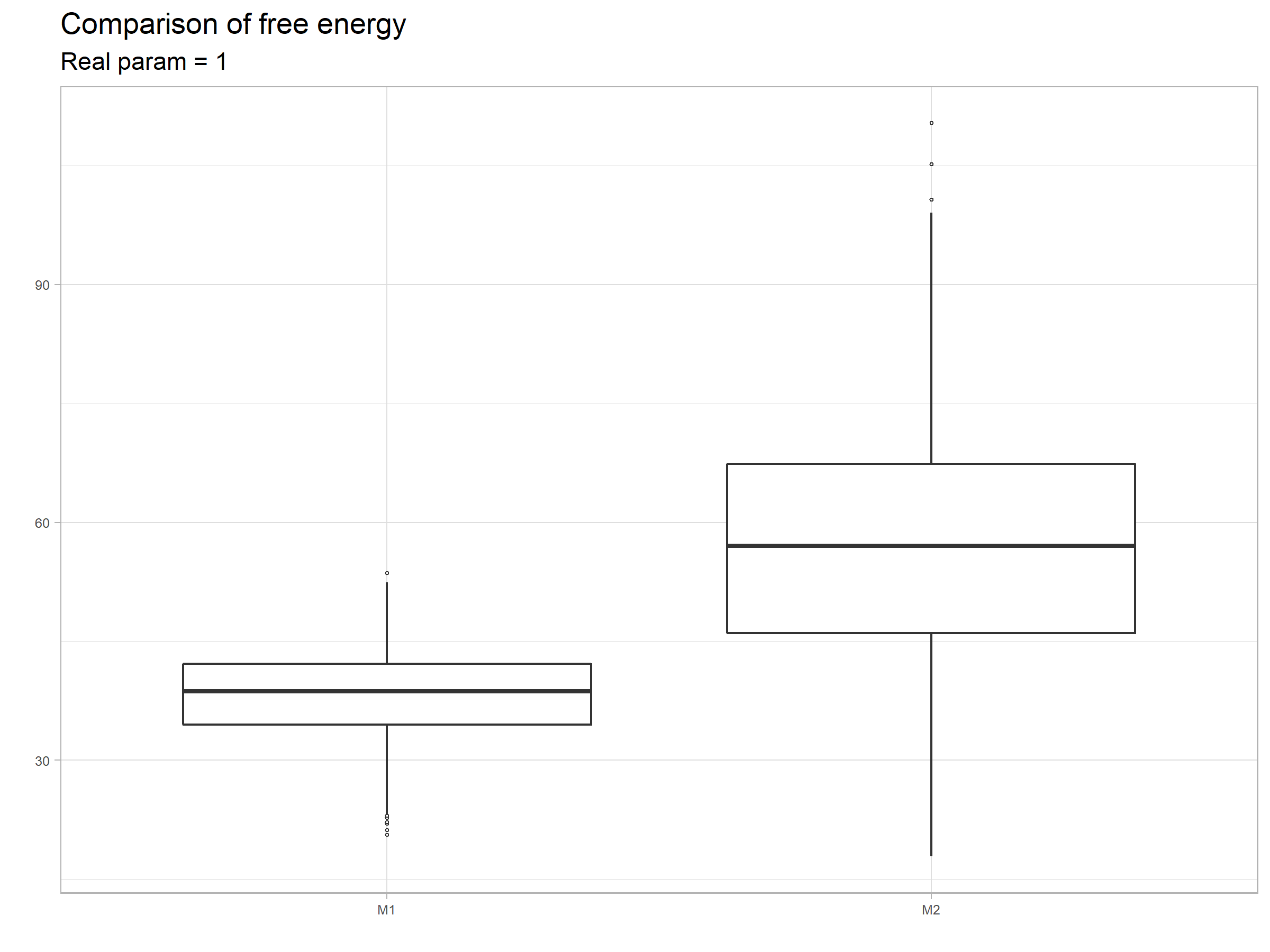
モデル1の方が自由エネルギーがが小さい傾向にあります。
解釈としては、事前分布を設定しない単純なモデルであるモデル2は、$\gamma=3$と真のモデルとパラメータがやや異なっているので、当てはまりが比較的悪いのに対し、事前分布を設定したより複雑なモデルであるモデル1は、モデル2に比較しより広い範囲の実現値をカバーできるため、ということになります。

一方、実現値をモデル2のパラメータ3に合わせた場合、結果は以下のように変わってきます。

$$ X^{30} \sim \mathrm{Exponential}(3) $$

今度はモデル2方が自由エネルギーが小さくなりました。このことから、自由エネルギーは、モデルを複雑にすれば小さくなりやすいというわけではなく、データの当てはまりが良い場合については、より単純なモデルほど小さくなる傾向にあることがわかります。

この傾向を再確認するため、実現値の数を$n=1$とし、実現値を0.1から3まで与えたときの2つのモデルの自由エネルギーを確認したところ、以下のような結果になりました。

単純なモデルであるモデル2が想定している値である0.1から0.8あたりまでが得られた場合、モデル2の自由エネルギーの方が小さくなり、それ以外の範囲では複雑なモデルであるモデル1の方が自由エネルギーが小さくなることが分かります。このことから、自由エネルギー（ベイズファクター）を用いたモデル評価では過学習（データにフィットするようむやみにモデルを複雑にし過ぎること）を抑えることができると言えます。またこの例からも分かるように、自由エネルギーがパラメーターに対し周辺化した値であることから、自由エネルギー（ベイズファクター）を用いたモデル評価では事前分布が大きく影響する、ということが分かります。

おわりに

以上、ベイズファクターについてみていきました。

ベイズファクターはパラメータに対し周辺化した尤度である周辺尤度に基づいて計算されますが、モデルの設定によってはこの計算が解析的に行えない場合があります。この場合、MCMCの結果からWBICを計算したり、ブリッジ・サンプリングを行うことで近似的に周辺尤度を計算する方法が提案されているようです。今後勉強し、まとめていこうと思っています。

また別の始点（汎化誤差）に着目したモデル評価の指標であるWAIC等についても、もう一度整理し投稿したいと思っています。

最後に、関数形の確認やシミュレーションの為に用いたRコードを載せておきます。


library(tidyverse)
library(ggplot2)

# ガンマ分布の形状を確認 -------------------------------------------------------------

#形状パラメータaを動かしたときのガンマ分布の確率密度

alpha <- seq(.5, 100, by=5)
p <- ggplot(data.frame(X=c(0, 40)), aes(x=X)) + theme_bw(base_size=11)+
  mapply(
    function(alpha,beta,co) geom_line(data=data.frame(X=x <- seq(0.1,40,0.05), Y=dgamma(x,shape=alpha,rate=beta)), aes(x=X,y=Y, color=co)),
    alpha,4,alpha) +
  coord_cartesian(ylim=c(0,0.75)) + labs(color="α", x="λ",y="Gamma(λ | α,β=4)")
p

#rateパラメータbを動かしたときのガンマ分布の確率密度

beta <- seq(.5, 10, by=.5)
p <- ggplot(data.frame(X=c(0, 40)), aes(x=X)) + theme_bw(base_size=11)+
  mapply(
    function(alpha,beta,co) geom_line(data=data.frame(X=x <- seq(0.1,6,0.01), Y=dgamma(x,shape=alpha,rate=beta)), aes(x=X,y=Y, color=co)),
    4,beta,beta) + labs(color="β", x="λ",y="Gamma(λ | α=4,β)")
p

# ガンマ分布のエントロピーを確認 -------------------------------------------------------------

H_gamma <- function(a, b){
  return(lgamma(a) + (1-a) * digamma(a) - log(b) + a)
}

# 形状パラメータaを動かしたとき

p <- ggplot() + geom_path(data=data.frame(X=x <- seq(0.1,100,0.1), Y=H_gamma(x,1)), aes(x=X,y=Y))

p <- ggplot() + theme_light(base_size=11) + mapply(
  function(beta,co) geom_path(data=data.frame(X=x <- seq(0.1,50,0.1), Y=H_gamma(x,beta)), aes(x=X,y=Y, color=co)),
  seq(0.01,10,len=20), seq(0.01,10,len=20)
  ) + labs(color="β", x="α",y="H(Gamma(α,β))")
p

#rateパラメータbを動かしたときのガンマ分布のエントロピー

p <- ggplot() + theme_light(base_size=11) + mapply(
  function(alpha,co) geom_path(data=data.frame(X=x <- seq(0.1,50,0.1), Y=H_gamma(alpha,x)), aes(x=X,y=Y, color=co)),
  seq(0.1,10,len=20), seq(0.1,10,len=20)
) + labs(color="α", x="β",y="H(Gamma(α,β))")
p

# ベイズファクターの計算 -------------------------------------------------------------

x <- round(rexp(5, 3),3)
x <- 0.01

F_model1 <- function(X,alpha,beta){
  return(-alpha*log(beta) -sum(log(seq(1, length(X)))) + (length(X) + alpha) * log(beta + sum(X)) )
}

F_model2 <- function(X, gamma){
  return( -length(X) * log(beta) + sum(X) * gamma )
}

gamma <- 3
alpha <- 3
beta <- 1


#計算結果
exp(-F_model1(X=x, alpha=alpha, beta=beta)
 + F_model2(X=x, gamma=gamma))

# lineplot ---------------------------------------------------------------

F_model1_p <- function(X,alpha,beta){
  return(-alpha*log(beta) + (1 + alpha) * log(beta + X) )
}

F_model2_p <- function(X, gamma){
  return( -1 * log(beta) + X * gamma )
}

p <- ggplot() + theme_light(base_size=11) + mapply(
    function(gamma) geom_line(data=data.frame(X=x2 <- seq(0.1,3,0.01), Y=F_model2_p(x2,gamma)), aes(x=X,y=Y,lty="model2")),
    gamma
  ) + mapply(
    function(alpha,beta) geom_line(data=data.frame(X=x2 <- seq(0.1,3,0.01), Y=F_model1_p(x2,alpha,beta)), aes(x=X,y=Y,lty="model1")),
    alpha,beta
  ) + labs(x="x",y="Free Energy")
p

# boxplot -----------------------------------------------------------------

n <- 30 #sample size

gamma_prime <- 1
set.seed(123)
m1 <- c()
m2 <- c()
for(i in 1:1000){
  x <- rexp(n,gamma_prime)
  m2[i] <- sum(-dexp(x,3,log=T))
  m1[i] <- F_model1(x,alpha=alpha,beta=beta)
}
mean(m1)
mean(m2)

plot_title <- ggtitle("Comparison of free energy",
                      sprintf("Real param = %.0f",gamma_prime))

p <- data_frame(M1=m1,M2=m2) %>%
  gather(key = "x",value = "y") %>%
  ggplot() +
  geom_boxplot(aes(x,y),lwd=0.5,outlier.shape = 21, outlier.size = 0.5) +
  theme_light() + xlab("") + ylab("") +
  theme(legend.text=element_text(size=4),
        legend.title=element_text(size=8,face="bold"),  
        axis.text=element_text(size=6),
        axis.title=element_text(size=8,face="bold"),
        strip.text.x = element_text(size=6,face="bold"),
        legend.position = "right") + plot_title
p
確率論 ベイズファクター

コメントを書く


※ コメントは承認されると表示されます

承認されたコメント一覧