はじめに
本記事ではベイズファクターを使った線形回帰モデルの評価方法を紹介します。
サンプルデータの分析
今回使用するサンプルデータはR標準的サンプルデータ、Attitudeです。 Attitudeは従業員が自信の所属する会社の評価に関する質問結果のデータで、ratingが会社の総合評価となります。以降は、会社の総合評価がどの要素によって説明されるのかをみていくことにします。
head(attitude)
# rating complaints privileges learning raises critical advance
# 1 43 51 30 39 61 92 45
# 2 63 64 51 54 63 73 47
# 3 71 70 68 69 76 86 48
# 4 61 63 45 47 54 84 35
# 5 81 78 56 66 71 83 47
# 6 43 55 49 44 54 49 34
尤度に基づく線形回帰分析
従来通りの手法としては尤度に基づく線形回帰分析があります。まずは何も考えずに全説明変数を用いて分析にかけてみましょう。
d <- attitude
res_full <- lm(rating~. , data=d)
summary(res_full)
# Call:
# lm(formula = rating ~ ., data = d)
#
# Residuals:
# Min 1Q Median 3Q Max
# -10.9418 -4.3555 0.3158 5.5425 11.5990
#
# Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 10.78708 11.58926 0.931 0.361634
# complaints 0.61319 0.16098 3.809 0.000903 ***
# privileges -0.07305 0.13572 -0.538 0.595594
# learning 0.32033 0.16852 1.901 0.069925 .
# raises 0.08173 0.22148 0.369 0.715480
# critical 0.03838 0.14700 0.261 0.796334
# advance -0.21706 0.17821 -1.218 0.235577
# ---
# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#
# Residual standard error: 7.068 on 23 degrees of freedom
# Multiple R-squared: 0.7326, Adjusted R-squared: 0.6628
# F-statistic: 10.5 on 6 and 23 DF, p-value: 1.24e-05
complaintsの正の傾きのみに対し十分小さいp値が得られ、他の変数のp値は有意でないという結果が得られました。
ここで、p値が示す意味には注意が必要です。回りくどい表現になってしまいますが、p値の意味は「係数が0と仮定したとき、新たにデータを取るとt分布に従う検定統計量がこれより極端な値をとる確率」となります。簡単にいうと各係数を採用する積極的な証拠を与えていないんです。
ともあれ、complaints以外の変数は消去の余地がありそうですが、尤度に基づく方法でのモデル選択にはAIC(赤池情報量基準)がよく使用されます。
$$ \mathrm{AIC} = -2×最大対数尤度 + 2×自由パラメータ数 \tag{1} $$
AICを小さくするモデルほど良いモデルとされます。また冗長なモデルには第2項の自由パラメータ数によってペナルティが与えられます。
step(res_full)
# Start: AIC=123.36
# rating ~ complaints + privileges + learning + raises + critical +
# advance
#
# Df Sum of Sq RSS AIC
# - critical 1 3.41 1152.4 121.45
# - raises 1 6.80 1155.8 121.54
# - privileges 1 14.47 1163.5 121.74
# - advance 1 74.11 1223.1 123.24
# <none> 1149.0 123.36
# - learning 1 180.50 1329.5 125.74
# - complaints 1 724.80 1873.8 136.04
#
# Step: AIC=121.45
# rating ~ complaints + privileges + learning + raises + advance
#
# Df Sum of Sq RSS AIC
# - raises 1 10.61 1163.0 119.73
# - privileges 1 14.16 1166.6 119.82
# - advance 1 71.27 1223.7 121.25
# <none> 1152.4 121.45
# - learning 1 177.74 1330.1 123.75
# - complaints 1 724.70 1877.1 134.09
#
# Step: AIC=119.73
# rating ~ complaints + privileges + learning + advance
#
# Df Sum of Sq RSS AIC
# - privileges 1 16.10 1179.1 118.14
# - advance 1 61.60 1224.6 119.28
# <none> 1163.0 119.73
# - learning 1 197.03 1360.0 122.42
# - complaints 1 1165.94 2328.9 138.56
#
# Step: AIC=118.14
# rating ~ complaints + learning + advance
#
# Df Sum of Sq RSS AIC
# - advance 1 75.54 1254.7 118.00
# <none> 1179.1 118.14
# - learning 1 186.12 1365.2 120.54
# - complaints 1 1259.91 2439.0 137.94
#
# Step: AIC=118
# rating ~ complaints + learning
#
# Df Sum of Sq RSS AIC
# <none> 1254.7 118.00
# - learning 1 114.73 1369.4 118.63
# - complaints 1 1370.91 2625.6 138.16
#
# Call:
# lm(formula = rating ~ complaints + learning, data = d)
#
# Coefficients:
# (Intercept) complaints learning
# 9.8709 0.6435 0.2112
AICに基づくステップワイズ法の結果、採用されたモデルは「rating ~ complaints + learning (+ 切片)」となりました。採用モデルのp値を確認してみましょう。
res_best <- lm(rating ~ complaints + learning, data=d)
summary(res_best)
# Call:
# lm(formula = rating ~ complaints + learning, data = d)
#
# Residuals:
# Min 1Q Median 3Q Max
# -11.5568 -5.7331 0.6701 6.5341 10.3610
#
# Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 9.8709 7.0612 1.398 0.174
# complaints 0.6435 0.1185 5.432 9.57e-06 ***
# learning 0.2112 0.1344 1.571 0.128
# ---
# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#
# Residual standard error: 6.817 on 27 degrees of freedom
# Multiple R-squared: 0.708, Adjusted R-squared: 0.6864
# F-statistic: 32.74 on 2 and 27 DF, p-value: 6.058e-08
complaintsは相も変わらず有意なp値が得られていますが、learningはモデルに含まれるもののp値は有意でありません。このデータは小サンプルなので、これだけで判断することは危険ですが、complaintsはratingの決定要因になっていると考えてよさそうです。
ベイズファクターによるモデル評価
一方のベイズファクターではどんな結果が得られるでしょうか。分析により、下記の通りベイズファクターが算出されたとしましょう。
Jeffreys(1961)
| model | $BF\lbrack \mathcal{\boldsymbol{M}}_ {\boldsymbol{\gamma}} : \mathcal{\boldsymbol{M}}_ {N} \rbrack$ |
|---|---|
| privileges | 3.177784 |
| learning | 103.393 |
| raises | 47.00917 |
| critical | 0.4493186 |
| advance | 0.4472295 |
| complaints + privileges | 75015.23 |
| $\vdots$ | $\vdots$ |
| complaints + privileges + learning + raises + critical | 3826.973 |
| complaints + privileges + learning + raises + advance | 7144.828 |
| complaints + privileges + learning + critical + advance | 6926.973 |
| complaints + privileges + raises + critical + advance | 1608.397 |
| complaints + learning + raises + critical + advance | 6461.751 |
| privileges + learning + raises + critical + advance | 51.02312 |
| complaints + privileges + learning + raises + critical + advance | 2211.912 |
このとき、どのように線形回帰モデルを評価していけるのか見ていきましょう。
モデル間比較
モデル間の比較には下記式を用います。これはEncompassing approachと呼ばれ、ベースとなるモデルの自由エネルギーを介して各モデルの自由エネルギーの大きさを評価するものです。
$$ BF\lbrack \mathcal{\boldsymbol{M}}_ {\boldsymbol{\gamma}^{'}} : \mathcal{\boldsymbol{M}}_ {\boldsymbol{\gamma}} \rbrack = \cfrac{BF\lbrack \mathcal{\boldsymbol{M}}_ {\boldsymbol{\gamma}^{'}} : \mathcal{\boldsymbol{M}}_ {N} \rbrack}{BF\lbrack \mathcal{\boldsymbol{M}}_ {\boldsymbol{\gamma}} : \mathcal{\boldsymbol{M}}_ {N} \rbrack} \tag{2} $$
モデルの冗長性は、パラメータの事前分布と真分布との乖離によって評価されます(モデル自体仮定のものだがここでは真の分布があるとする)。事前分布が、真の分布からおよそ離れた広範囲のパラメータ空間を考慮したものの場合、そのモデルの周辺尤度は0に近づくため、比較的説明力の低いモデルと判断されやすくなってしまいます。
ベースとなるモデルをフルモデルとしたときの比較結果は次のようになります。

最も優れたモデルはcomplaintsのみのモデルという結果になりました。complaintsのみのモデルとの比較ではフルモデルを決定的に否定するベイズファクターが得られています(Kass and Rafteryの指標参照)。一方、complaintsのみのモデルと、さらにlearningを加えた二番目に優れたモデルを比較するベイズファクター(「complaints」/「complaints + learning」 )は2.016となり、二番目のモデルを棄却する証拠はあまりあるとは言えない結果になりました。
これらの結果の優れているところは、モデルを積極的に肯定するエビデンス=周辺尤度を比較することでモデル間の比較をできることにあります。これはp値に基づく枠組みでは不可能でした。これについてはこちらも参照のこと。
説明変数の選択
モデル間比較ではなく、各説明変数が必要かどうかを知りたい、という場合もあると思います。その場合、ベースとなるモデルから確認したい変数1つだけを除いた(または追加した)モデルと、ベースモデルを、ベイズファクターによって比較するという方法が考えられます。
ベースモデルをフルモデルとしたとき、各変数を1個ずつ取り除いたモデルとの比較を行った結果を下に示します。
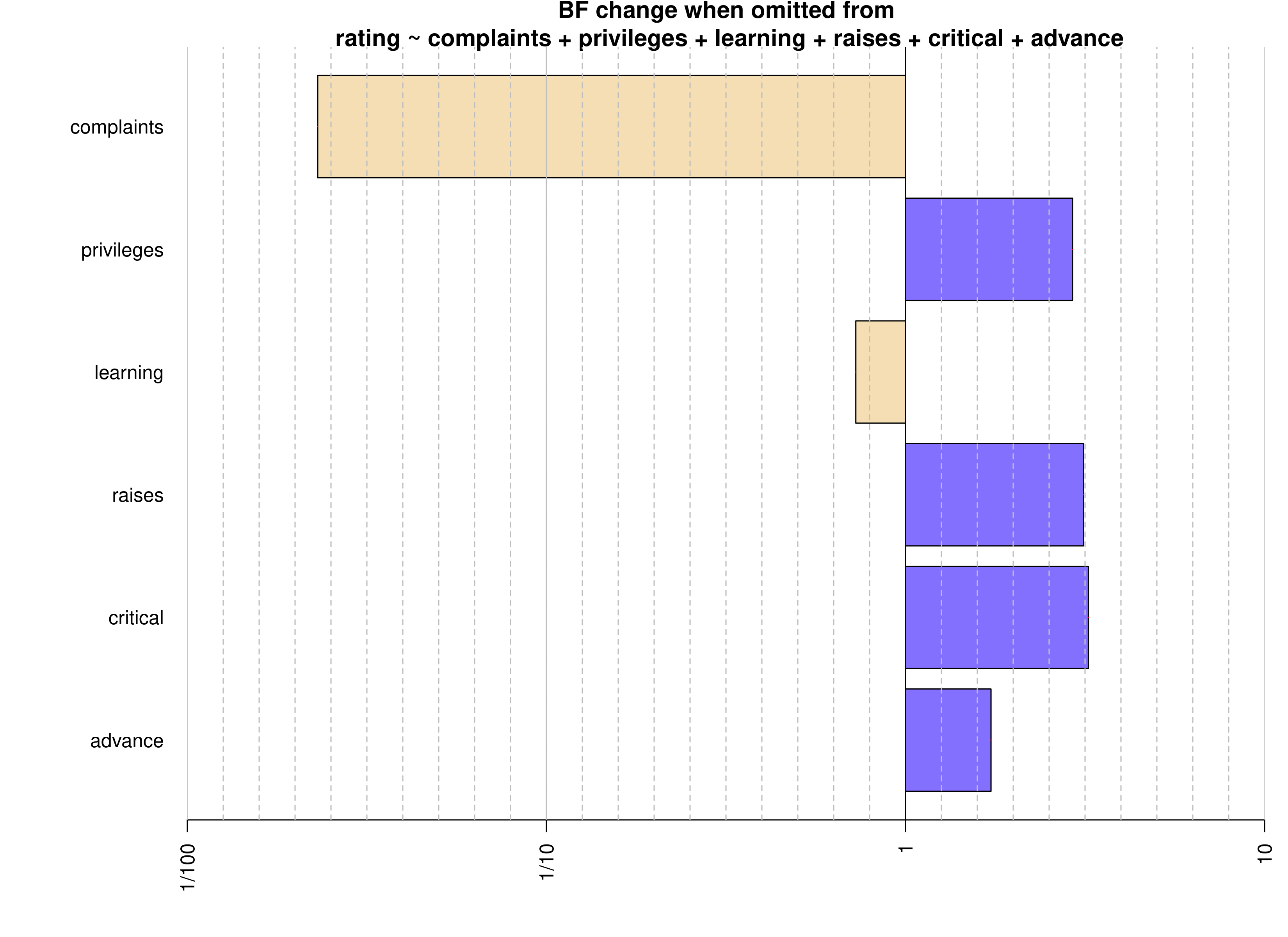
complaintsの必要性を測るベイズファクター(「フルモデル」/「フルモデル -complaints」 )は43.35と、強くcomplaintsを除いたモデルを棄却する結果となったため、complaintsはratingを説明するのに需要な指標と言えそうです。一方、それ以外の変数についてはあまり根拠があるとは言えない結果ばかりでした。
ベースモデルをヌルモデルとしたときの結果も下に示します。

complaintsについては決定的にヌルモデルを棄却する結果が得られています。またlearning、raises、privilegesについても肯定的な結果が得られています。あれ、じゃあこれら4つの変数を採用したモデルがいいのでは?…そうでもありません。この4変数を採用したモデルとフルモデルを比較したベイズファクターはそれほど大きくありません。ここには落とし穴があります。
下の表は7変数の相関関係を表しています。これを見ると、有力な変数complaintsは、上で挙げたlearning、raises、privilegesの3変数と有意に正の相関関係にあります。つまり、この3変数はcomplaintsのもつ傾向の一部分を表現できるために、ヌルモデルとの比較の際も肯定的な結果が得られていたのです。

あるモデルに相関関係が高い変数の組み合わせがあることを多重共線性と呼びます。多重共線性のあるモデルは係数の値が不安定となり、また冗長であるために望ましくないとされます。
ベイズファクターを用いたモデル間比較の場合、各変数に着目した比較よりも前節の全モデル間比較の手法の方が、より多重共線性に強い検討手法と言えそうです。
事後モデル確率の更新
ベイズファクターは、得られたデータのモデルへの当てはまりの良さを測る相対的な指標ですが、モデル自体を評価するものではありません。モデルを評価するためには、各モデル$\mathcal{\boldsymbol{M}}_ {\boldsymbol{\gamma}}$の事前確率$p\left(\mathcal{\boldsymbol{M}}_ {\boldsymbol{\gamma}}\right)$を、新しく得られたデータから算出したベイズファクターに基づき下記式のようにアップデートすることで、事後モデルオッズを導く必要があります。
$$ p(\mathcal{\boldsymbol{M}}_ {\boldsymbol{\gamma}} | \boldsymbol{Y}) = \cfrac{p(\mathcal{\boldsymbol{M}}_ {\boldsymbol{\gamma}})BF\lbrack \mathcal{\boldsymbol{M}}_ {\boldsymbol{\gamma}} : \mathcal{\boldsymbol{M}}_ {b}\rbrack}{\sum_ {\boldsymbol{\gamma}^{'}} p(\mathcal{\boldsymbol{M}}_ {\boldsymbol{\gamma}^{'}})BF\lbrack \mathcal{\boldsymbol{M}}_ {\boldsymbol{\gamma}^{'}} : \mathcal{\boldsymbol{M}}_b \rbrack} \tag{3} $$
事前モデルオッズは、データに完全依存して決定されるベイズファクターとは対照的に、データとは無関係に事前に想定するモデル確率の組み合わせで決定されます。もしあるモデルが何らかの確証のもったメカニズムを背景に持つ場合、そのモデル確率を分子とした事前モデルオッズは大きくなるでしょう。逆に、なんのメカニズムも想定されない無関係な変数同士の関係性を表現したモデルなんかの確率を分子とした事前モデルオッズは、相対的に小さくするべきです。
このように、事前モデルオッズは、データを取る前から分かりきっているような情報や意見を事後モデルオッズに与える役目をもちます。
Attitudeに対し、得られたベイズファクターと事前モデルオッズを基に事後モデルオッズを算出した結果(TOP6)を下記に示します。ここで、事前モデルオッズはモデル間で一律としました。
| model | $p(\mathcal{\boldsymbol{M}}_ {\boldsymbol{\gamma}} \mid \boldsymbol{Y})$ |
|---|---|
| complaints | 0.296 |
| complaints + learning | 0.147 |
| complaints + learning + advance | 0.062 |
| complaints + raises | 0.055 |
| complaints + privileges | 0.053 |
| complaints + advance | 0.052 |
事前モデルオッズを一定にした場合、事後モデルオッズはあるモデルの周辺尤度と全モデルの周辺尤度和の比となります。
表から読み取れるように、最も大きい周辺尤度を持つComplaintsのみのモデルが最も事後モデル確率が大きく、全体の約3割を占めました。
BayesFactorパッケージを使ったベイズファクターの計算
最後に、R言語で簡単にベイズファクターを求める方法を載せて終わりにします。
ベイズファクターの計算にはMoreyさんの作成したBayesFactorパっケージが直感的に使えて便利です。これまでの節で示したAttitudeデータのベイズファクターも、このパッケージを使って算出したものになります。
下のスクリプトは単純にAttitudeデータでベイズファクターを求めたものです。
library(BayesFactor)
bf <- regressionBF(rating ~ ., data=d, rscaleCont = "medium")
bf
# Bayes factor analysis
# --------------
# [1] complaints : 417938.6 ±0.01%
# [2] privileges : 3.177784 ±0%
# [3] learning : 103.393 ±0%
# [4] raises : 47.00917 ±0.01%
# [5] critical : 0.4493186 ±0%
# [6] advance : 0.4472295 ±0%
# [58] complaints + privileges + learning + raises + advance : 7144.828 ±0%
# ~~略~~
# [59] complaints + privileges + learning + critical + advance : 6926.973 ±0%
# [60] complaints + privileges + raises + critical + advance : 1608.397 ±0%
# [61] complaints + learning + raises + critical + advance : 6461.751 ±0%
# [62] privileges + learning + raises + critical + advance : 51.02312 ±0%
# [63] complaints + privileges + learning + raises + critical + advance : 2211.912 ±0%
#
# Against denominator:
# Intercept only
# ---
# Bayes factor type: BFlinearModel, JZS
下のスクリプトは説明変数の選択を目的とした分析をしています。
bf2 = regressionBF(rating ~ ., data = attitude, whichModels = "top")
bf2
# Bayes factor top-down analysis
# --------------
# When effect is omitted from complaints + privileges + learning + raises + critical + advance , BF is...
# [1] Omit advance : 1.730165 ±0%
# [2] Omit critical : 3.230159 ±0%
# [3] Omit raises : 3.131667 ±0%
# [4] Omit learning : 0.7271523 ±0%
# [5] Omit privileges : 2.921341 ±0%
# [6] Omit complaints : 0.02306743 ±0%
#
# Against denominator:
# rating ~ complaints + privileges + learning + raises + critical + advance
# ---
# Bayes factor type: BFlinearModel, JZS
bf3 = regressionBF(rating ~ ., data = attitude, whichModels = "bottom")
bf3
# Bayes factor analysis
# --------------
# [1] complaints : 417938.6 ±0.01%
# [2] privileges : 3.177784 ±0%
# [3] learning : 103.393 ±0%
# [4] raises : 47.00917 ±0.01%
# [5] critical : 0.4493186 ±0%
# [6] advance : 0.4472295 ±0%
#
# Against denominator:
# Intercept only
# ---
# Bayes factor type: BFlinearModel, JZS
下のスクリプトでは事前モデルオッズを一定としたときの事後モデルオッズを算出しています。
prior.odds <- newPriorOdds(bf, type="equal")
post.odds = prior.odds * bf
post.prob = as.BFprobability(post.odds)
head(post.prob)
# Posterior probabilities
# --------------
# [1] complaints : 0.296141 ±NA%
# [2] complaints + learning : 0.1468678 ±NA%
# [3] complaints + learning + advance : 0.06238406 ±NA%
# [4] complaints + raises : 0.05491387 ±NA%
# [5] complaints + privileges : 0.05315394 ±NA%
# [6] complaints + advance : 0.05155578 ±NA%
#
# Normalized probability: 0.6650164
# ---
# Model type: BFlinearModel, JZS
まとめ
本記事ではベイズファクターを使った線形回帰モデルの評価方法を紹介しました。
こちらの記事では線形回帰分析での客観ベイズ的な事前分布の設定方法等、理論を少し詳しく説明しています。
こちらの記事ではベイズファクターを推定するための手法を複数実践しているので、読んでみてください。
