はじめに
今回は、以前の記事で紹介したRidge回帰とLasso回帰をRのパッケージglmnetで試してみます。さらにRstanを用いてBayesian RigdeとBayesian Lasso を実装して、glmnetの結果との比較をしてみたいと思います。
目次は以下のとおりです。
glmnetを用いた正則化回帰
こちらのサイトを参考にglmnetを用いて正則化回帰をします。
下準備
まずはデータの準備を。BostonHousingにはボストンの住宅506件について、住宅の価格medvおよび13の変数が格納されています。ここでは、medvを13の変数で説明する回帰を考えます。
library(mlbench)
library(tidyverse)
data("BostonHousing")
head(BostonHousing)
## crim zn indus chas nox rm age dis rad tax ptratio b lstat medv
## 1 0.00632 18 2.31 0 0.538 6.575 65.2 4.0900 1 296 15.3 396.90 4.98 24.0
## 2 0.02731 0 7.07 0 0.469 6.421 78.9 4.9671 2 242 17.8 396.90 9.14 21.6
## 3 0.02729 0 7.07 0 0.469 7.185 61.1 4.9671 2 242 17.8 392.83 4.03 34.7
## 4 0.03237 0 2.18 0 0.458 6.998 45.8 6.0622 3 222 18.7 394.63 2.94 33.4
## 5 0.06905 0 2.18 0 0.458 7.147 54.2 6.0622 3 222 18.7 396.90 5.33 36.2
## 6 0.02985 0 2.18 0 0.458 6.430 58.7 6.0622 3 222 18.7 394.12 5.21 28.7
predictors = BostonHousing %>% select(-medv) %>% data.matrix()
predictors_std <- scale(predictors)
response_variable <- BostonHousing$medv
response_variable_std <- scale(response_variable)
Rのパッケージlmを使って通常の線形回帰もしてみます。
res <- lm(response_variable_std ~ predictors_std)
summary(res)
## Call:
## lm(formula = response_variable_std ~ predictors_std)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.69559 -0.29680 -0.05633 0.19322 2.84864
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -1.620e-16 2.294e-02 0.000 1.000000
## predictors_stdcrim -1.010e-01 3.074e-02 -3.287 0.001087 **
## predictors_stdzn 1.177e-01 3.481e-02 3.382 0.000778 ***
## predictors_stdindus 1.534e-02 4.587e-02 0.334 0.738288
## predictors_stdchas 7.420e-02 2.379e-02 3.118 0.001925 **
## predictors_stdnox -2.238e-01 4.813e-02 -4.651 4.25e-06 ***
## predictors_stdrm 2.911e-01 3.193e-02 9.116 < 2e-16 ***
## predictors_stdage 2.119e-03 4.043e-02 0.052 0.958229
## predictors_stddis -3.378e-01 4.567e-02 -7.398 6.01e-13 ***
## predictors_stdrad 2.897e-01 6.281e-02 4.613 5.07e-06 ***
## predictors_stdtax -2.260e-01 6.891e-02 -3.280 0.001112 **
## predictors_stdptratio -2.243e-01 3.080e-02 -7.283 1.31e-12 ***
## predictors_stdb 9.243e-02 2.666e-02 3.467 0.000573 ***
## predictors_stdlstat -4.074e-01 3.938e-02 -10.347 < 2e-16 ***
## ---
## Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
##
## Residual standard error: 0.516 on 492 degrees of freedom
## Multiple R-squared: 0.7406, Adjusted R-squared: 0.7338
## F-statistic: 108.1 on 13 and 492 DF, p-value: < 2.2e-16
Lasso回帰
以前の記事と同様に記号を定義したとき、
glmnet::glmnet(alpha, lambda)は下記式に基づいて係数パラメータ
glmnet::glmnet(alpha=1)でlambdaはlambdaの値は交差検証法を行うglmet::cv.glmet()でnfolds=nrow(BostonHousing)とすることにより1個抜き交差検証法を行い決定します。
簡単にRスクリプトと結果だけ。
library(glmnet)
lambdas <- 10^seq(1, -3, by = -.1)
# alpha=1でLasso回帰
fit_std <- glmnet(predictors_std, response_variable_std, alpha = 1, lambda = lambdas)
lambda_calc <- cv.glmnet(predictors_std, response_variable_std, alpha = 1, lambda = lambdas, nfolds = nrow(BostonHousing), grouped = FALSE)
optlambda <- lambda_calc$lambda.min
log(optlambda)
## [1] -6.21698 Lasso回帰の結果
coef(fit_std, s = optlambda)
## Lassoの結果
## 14 x 1 sparse Matrix of class "dgCMatrix"
## 1
## (Intercept) -8.076217e-16
## crim -9.513801e-02
## zn 1.089273e-01
## indus .
## chas 7.448868e-02
## nox -2.100694e-01
## rm 2.937399e-01
## age .
## dis -3.272420e-01
## rad 2.541077e-01
## tax -1.920829e-01
## ptratio -2.202126e-01
## b 9.048729e-02
## lstat -4.057165e-01
# 結果の描画 -------------------------------------------------------------------
res_lm <- res$coefficients %>% as.data.frame() %>% cbind(variable = rownames(.)) %>%
mutate(variable = str_replace(variable, pattern = "predictors_std", replacement = "")) %>%
rename("value" = ".") %>% filter(variable != "(Intercept)")
names(lambdas) <- paste0("s",seq(0,40))
res_lasso <- as.matrix(fit_std$beta) %>% as.data.frame()%>% cbind(variable = rownames(.)) %>%
pivot_longer(cols=-variable , names_to = "x", values_to="value") %>%
mutate(lambda = lambdas[x], x=NULL)
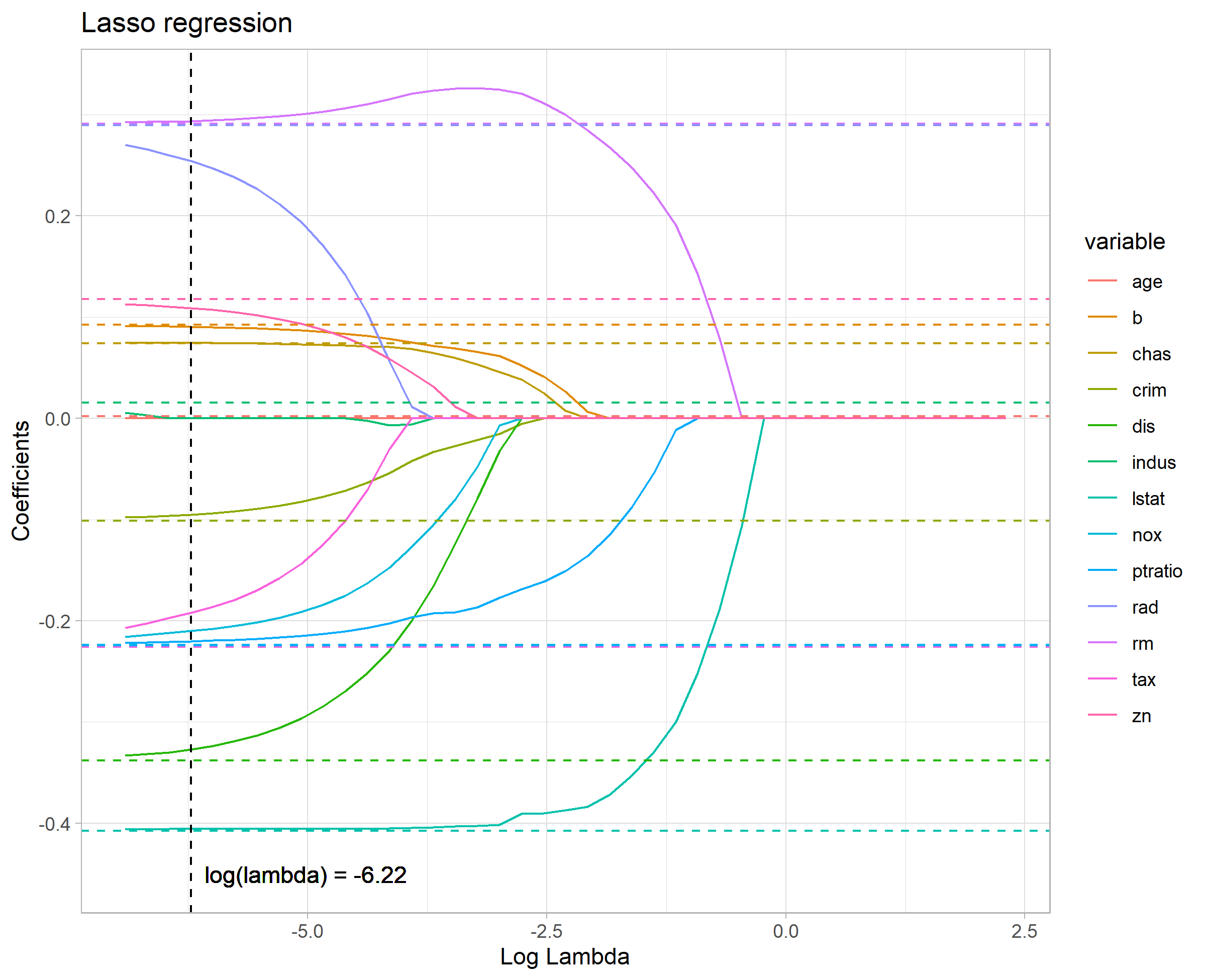
p <- ggplot(data = res_lasso, aes(x=log(lambda), y=value, group=variable, color=variable)) +
theme_light(base_size=11) + geom_line() +
labs(x="Log Lambda", y= "Coefficients", title="Lasso regression") +
geom_hline(data=res_lm, aes(yintercept=value, col=variable), linetype="dashed") +
geom_vline(aes(xintercept = log(optlambda)), linetype="dashed") +
geom_text(aes(x=log(optlambda)+1.2, y=-0.45, label=sprintf("log(lambda) = %.2f", log(optlambda))), color="black")
結果の図には13の変数に対する標準化偏回帰係数がindusとageの係数パラメータははやいうちから0となっており、変数の選択が行われていることが分かります。
Ridge回帰
Lasso回帰のときとほぼ同様ですが、glmnet::glmnet(alpha=0)で
同様にして…
# alpha=0でRidge回帰
fit_std <- glmnet(predictors_std, response_variable_std, alpha = 0, lambda = lambdas) # Ridge
lambda_calc <- cv.glmnet(predictors_std, response_variable_std, alpha = 0, lambda = lambdas,nfolds = nrow(BostonHousing), grouped = FALSE)
## ~(略)~
log(optlambda)
## [1] -4.60517 Ridge回帰の結果
coef(fit_std, s = optlambda)
## Ridgeの結果
## 14 x 1 sparse Matrix of class "dgCMatrix"
## 1
## (Intercept) -8.075655e-16
## crim -9.662095e-02
## zn 1.100420e-01
## indus 3.501806e-03
## chas 7.587874e-02
## nox -2.090907e-01
## rm 2.953197e-01
## age -1.009341e-03
## dis -3.236125e-01
## rad 2.537157e-01
## tax -1.929854e-01
## ptratio -2.198235e-01
## b 9.215636e-02
## lstat -4.006555e-01
結果の図からはLasso回帰と同様、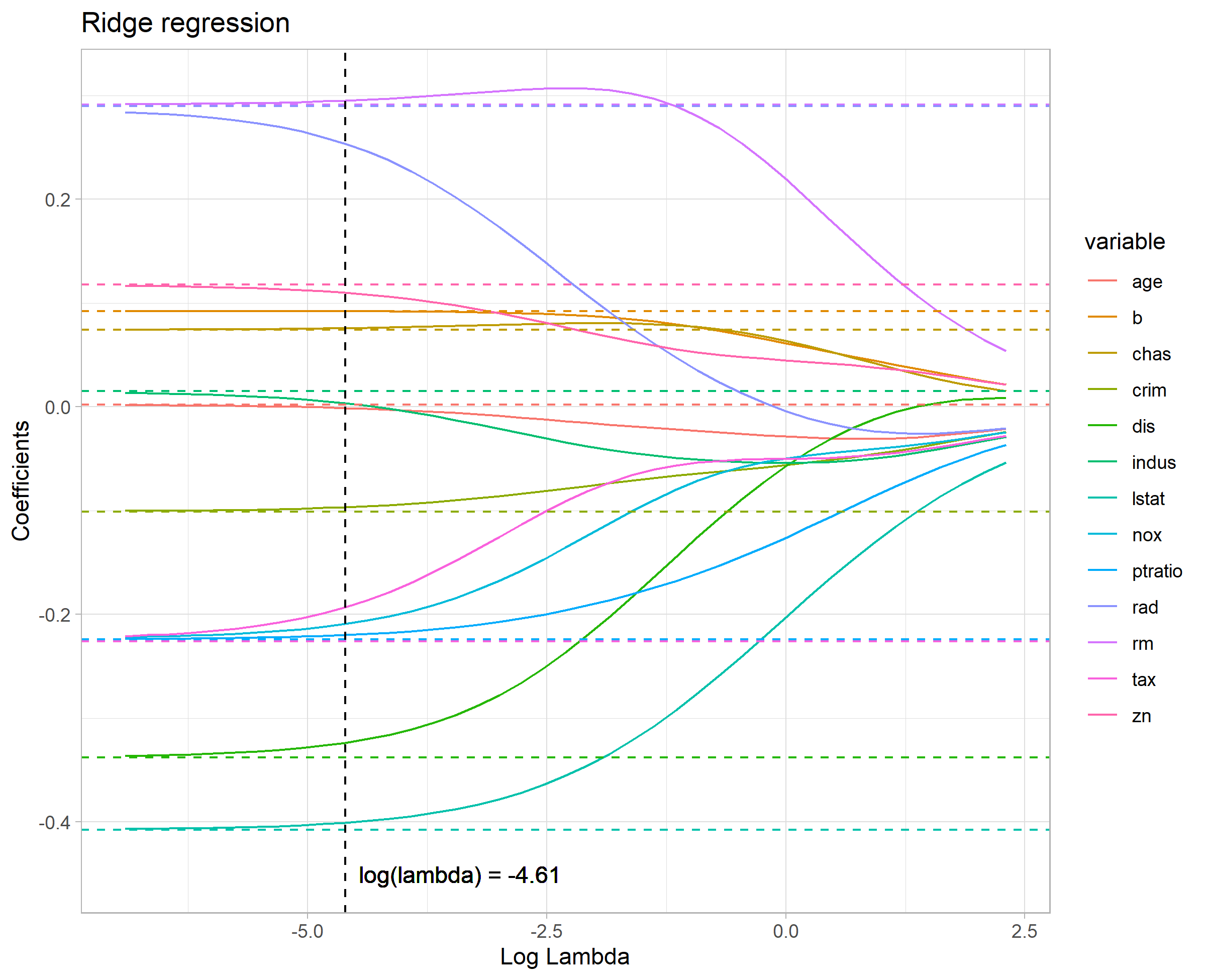
rstanを用いた正則化回帰
以前の記事後半を参考に、rstanを用いて今までの正則化回帰と同様の分析を再現します。
Lasso回帰
lambdaの計算だけ注意が必要です。
実装
//model_lasso.stan
data{
int N; //標本数
int H; //説明変数の数(切片を除く)
vector[N] y; //目的変数 標準化済み
matrix[N,H] x; // 説明変数 標準化済み
}
parameters{
real w_0;
vector[H] w; //係数パラメータ
real<lower=0> sigma;
real<lower=0> b;
}
transformed parameters{
vector[N] mu;
mu = w_0 + x * w;
}
model{
y ~ normal(mu, sigma);
w ~ double_exponential(0, b);
}
generated quantities{
real log_lambda;
log_lambda = log(sigma^2 / (N * b)); //(7)式
}
結果
以下で上記Stanファイルを走らせます。
data <- list(N=nrow(BostonHousing), H=ncol(predictors_std), y=as.vector(response_variable_std), x=predictors_std)
stanmodel_lasso <- stan_model("model_lasso.stan")
rstan_options(auto_write = TRUE)
options(mc.cores = parallel::detectCores())
fit_lasso <- sampling(stanmodel_lasso, data=data, iter=2500, warmup=500, chain=4)
print(fit_lasso, pars=c("w_0","w","log_lambda"))
## Inference for Stan model: model_lasso.
## 4 chains, each with iter=2500; warmup=500; thin=1;
## post-warmup draws per chain=2000, total post-warmup draws=8000.
##
## mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
## w_0 0.00 0 0.02 -0.05 -0.02 0.00 0.02 0.04 8915 1
## w[1] -0.09 0 0.03 -0.15 -0.11 -0.09 -0.07 -0.03 9311 1
## w[2] 0.11 0 0.03 0.04 0.08 0.11 0.13 0.17 7094 1
## w[3] 0.00 0 0.04 -0.08 -0.03 0.00 0.03 0.08 7595 1
## w[4] 0.07 0 0.02 0.03 0.06 0.07 0.09 0.12 8469 1
## w[5] -0.21 0 0.05 -0.30 -0.24 -0.21 -0.17 -0.11 6364 1
## w[6] 0.30 0 0.03 0.23 0.27 0.30 0.32 0.36 6917 1
## w[7] 0.00 0 0.04 -0.07 -0.03 0.00 0.02 0.08 8055 1
## w[8] -0.32 0 0.05 -0.41 -0.35 -0.32 -0.29 -0.23 7513 1
## w[9] 0.24 0 0.06 0.12 0.20 0.24 0.29 0.37 5429 1
## w[10] -0.18 0 0.07 -0.32 -0.23 -0.18 -0.14 -0.05 5855 1
## w[11] -0.22 0 0.03 -0.28 -0.24 -0.22 -0.20 -0.16 7772 1
## w[12] 0.09 0 0.03 0.04 0.07 0.09 0.11 0.14 8959 1
## w[13] -0.40 0 0.04 -0.48 -0.43 -0.40 -0.38 -0.33 7017 1
## log_lambda -5.93 0 0.31 -6.57 -6.14 -5.92 -5.71 -5.36 7056 1
係数パラメータの事後分布はglmnet()による結果と概ね整合しているようです。ただし、glmnet()によるLassoでは一部の係数パラメータが0となり、変数選択が可能であったのに対し、Bayesian Lassoでは中央値0付近の事後分布が得られるので、変数選択は難しくなります。
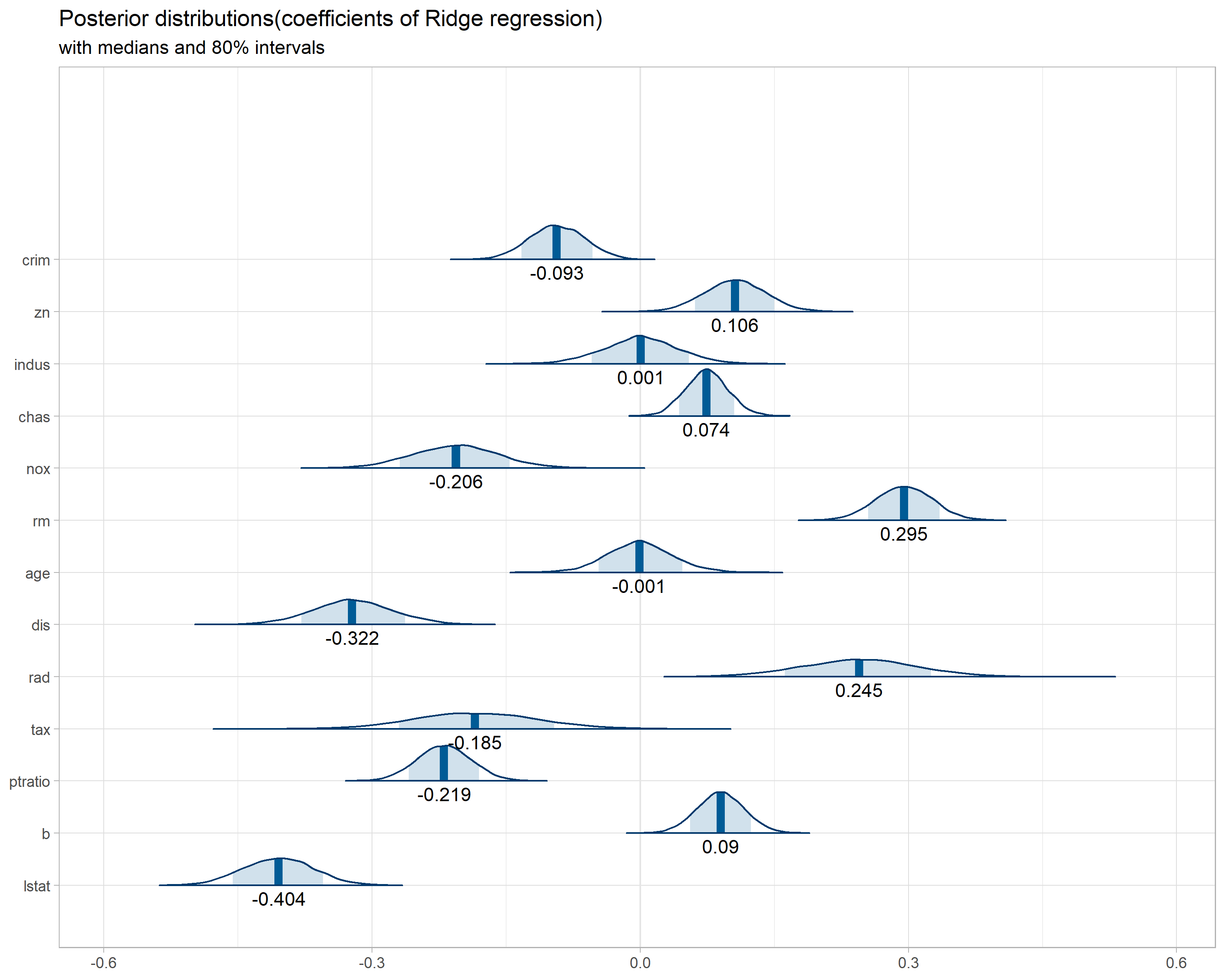
glmnet()では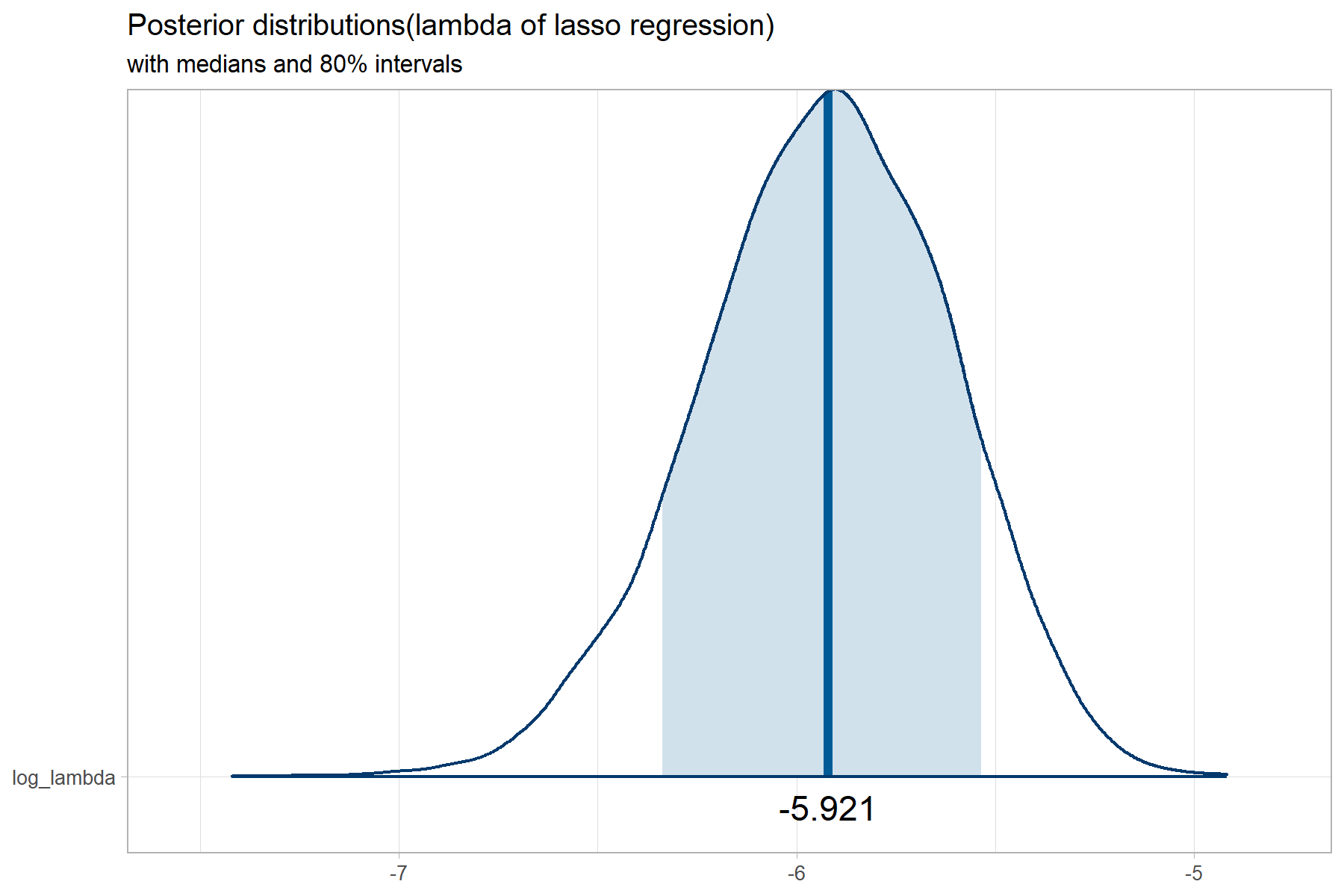
結果の描画のためのRスクリプトは以下になります。
library(bayesplot)
# 係数パラメータの事後分布の描画(lasso) ---------------------------------------------------------
w_id <- c(colnames(predictors))
names(w_id) <- c(sprintf("w[%.0f]", seq(1,13,by=1)))
posterior <- as.matrix(fit_lasso) %>% as.data.frame() %>% select(starts_with("w["))
colnames(posterior) <- w_id[colnames(posterior)]
par_median <- posterior %>% summarise_all(list(median)) %>% summarise_all(list(round),digits=3) %>% pivot_longer(everything())
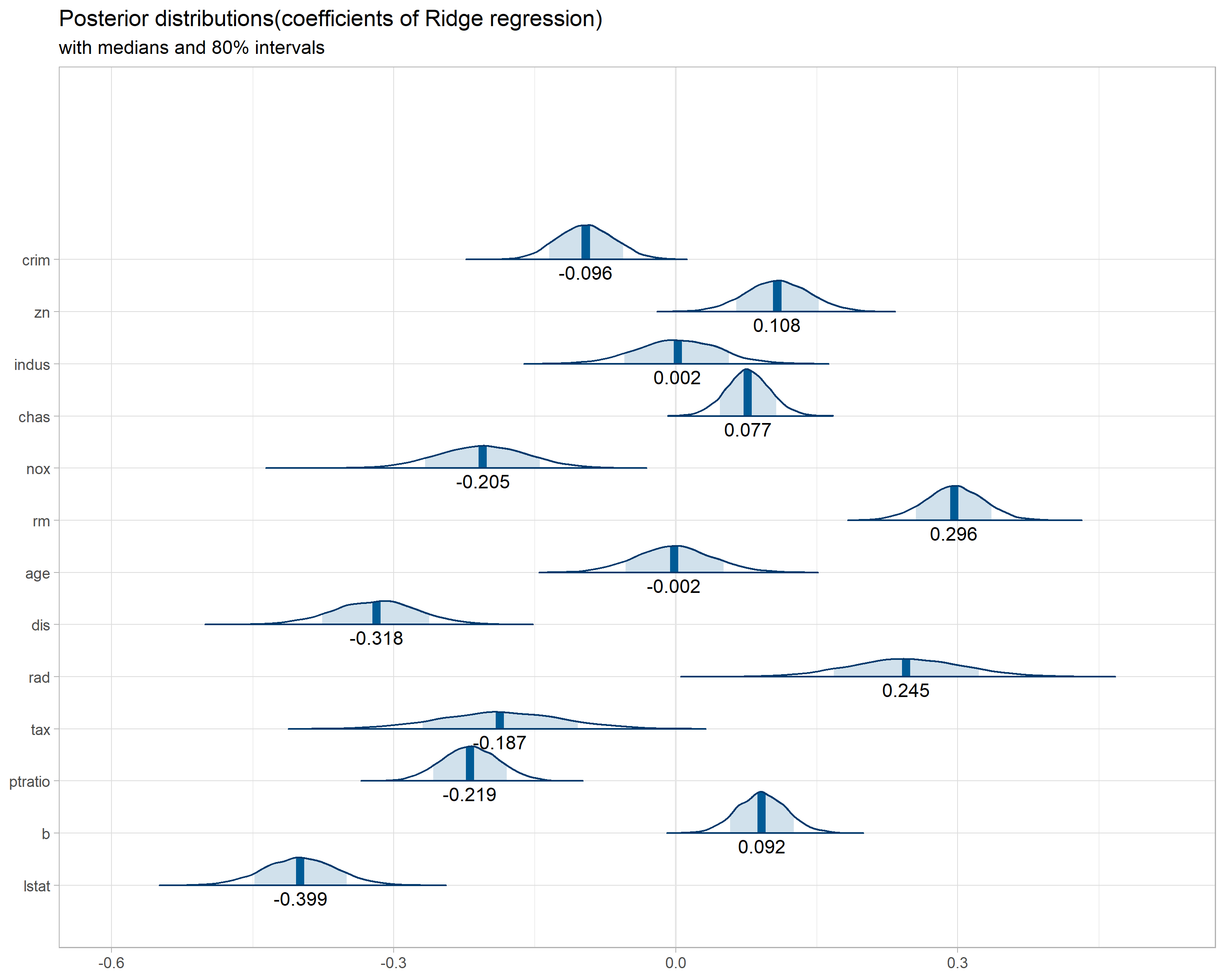
plot_title <- ggtitle("Posterior distributions(coefficients of Ridge regression)",
"with medians and 80% intervals")
p <- mcmc_areas(posterior,
prob = 0.8) + plot_title + theme_light(base_size=11) +
geom_text(data=par_median, aes(x=value, y=name, label=value), nudge_y = -0.25)
# lambdaの事後分布の描画(lasso) ----------------------------------------------------------
posterior <- as.matrix(fit_lasso) %>% as.data.frame() %>% select(log_lambda)
par_median <- posterior %>% summarise_all(list(median)) %>% summarise_all(list(round),digits=3) %>% pivot_longer(everything())
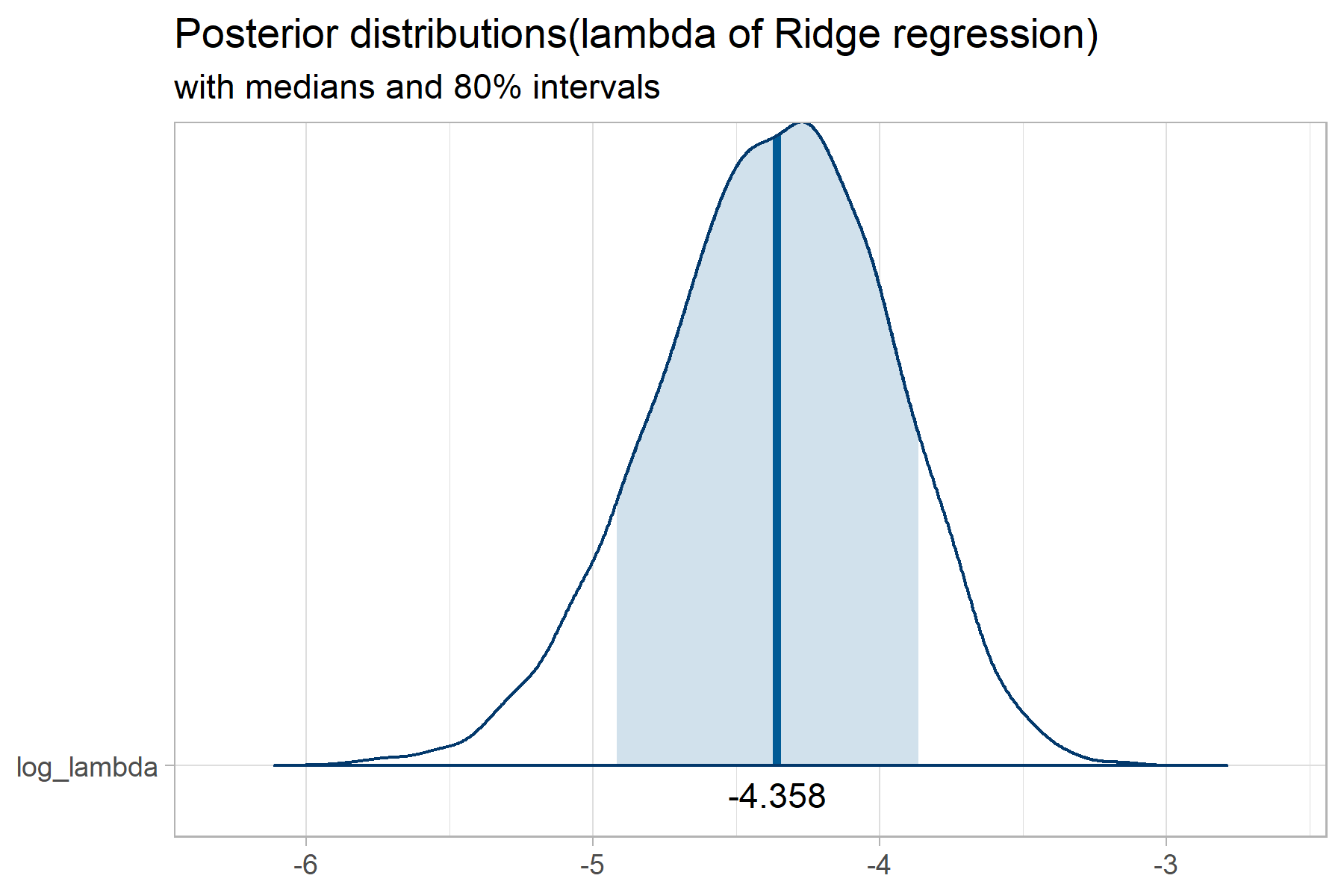
plot_title <- ggtitle("Posterior distributions(lambda of lasso regression)",
"with medians and 80% intervals")
p <- mcmc_areas(posterior,
prob = 0.8) + plot_title + theme_light(base_size=8) +
geom_text(data=par_median, aes(x=value, y=name, label=value), nudge_y = -0.04)
Ridge回帰
lambdaの計算方法は下記の通りです。
実装
//model_ridge.stan
data{
int N; //標本数
int H; //説明変数の数(切片を除く)
vector[N] y; //目的変数 標準化済み
matrix[N,H] x; // 説明変数 標準化済み
}
parameters{
real w_0;
vector[H] w; //係数パラメータ
real<lower=0> sigma;
real<lower=0> rho;
}
transformed parameters{
vector[N] mu;
mu = w_0 + x * w;
}
model{
y ~ normal(mu, sigma);
w ~ normal(0, (1 / sqrt(rho)));
}
generated quantities{
real log_lambda;
log_lambda = log( rho * sigma^2 / N ); //(11)式
}
結果
以下で上記Stanファイルを走らせます。
stanmodel_ridge <- stan_model("model_ridge.stan")
rstan_options(auto_write = TRUE)
options(mc.cores = parallel::detectCores())
fit_ridge <- sampling(stanmodel_ridge, data=data, iter=2500, warmup=500, chain=4)
print(fit_ridge, pars=c("w_0","w","log_lambda"))
## Inference for Stan model: model_ridge.
## 4 chains, each with iter=2500; warmup=500; thin=1;
## post-warmup draws per chain=2000, total post-warmup draws=8000.
##
## mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
## w_0 0.00 0 0.02 -0.04 -0.02 0.00 0.02 0.04 9413 1
## w[1] -0.10 0 0.03 -0.15 -0.12 -0.10 -0.07 -0.03 9737 1
## w[2] 0.11 0 0.03 0.04 0.09 0.11 0.13 0.17 6719 1
## w[3] 0.00 0 0.04 -0.08 -0.03 0.00 0.03 0.09 7186 1
## w[4] 0.08 0 0.02 0.03 0.06 0.08 0.09 0.12 8970 1
## w[5] -0.21 0 0.05 -0.30 -0.24 -0.21 -0.17 -0.11 6529 1
## w[6] 0.30 0 0.03 0.23 0.28 0.30 0.32 0.36 6418 1
## w[7] 0.00 0 0.04 -0.08 -0.03 0.00 0.02 0.08 7222 1
## w[8] -0.32 0 0.04 -0.41 -0.35 -0.32 -0.29 -0.23 5893 1
## w[9] 0.25 0 0.06 0.13 0.21 0.25 0.29 0.36 5012 1
## w[10] -0.19 0 0.06 -0.31 -0.23 -0.19 -0.14 -0.06 5198 1
## w[11] -0.22 0 0.03 -0.28 -0.24 -0.22 -0.20 -0.16 7225 1
## w[12] 0.09 0 0.03 0.04 0.07 0.09 0.11 0.14 7857 1
## w[13] -0.40 0 0.04 -0.47 -0.43 -0.40 -0.37 -0.32 6705 1
## log_lambda -4.38 0 0.41 -5.23 -4.64 -4.36 -4.09 -3.65 7454 1
係数パラメータの事後分布はglmnet()による結果と概ね整合しているようです。
まとめ
損失関数に係数パラメータのノルム分ペナルティを加えることによる通常の正則化回帰と、Bayesian正則化回帰の整合性を実験により確認することができました。まあまあ楽しかったです。
実用上の観点から両者を比較すると、通常の正則化回帰は(特にLasso回帰の場合)係数パラメータが0に収束することを用いた変数選択が可能であることが強みです。一方Bayesian正則化回帰では、係数パラメータとともに、係数パラメータのノルム分ペナルティの重み
