はじめに
今回は分類についての記事です。 正規分布の混合モデルをによるsoft K-Means法を扱います。 タイトルにガウス過程とありますが、今回使用するデータが空間データなので、ガウス過程を用いて空間の近接性を考慮したクラスタリングにも挑戦しました、結果、うまくいかなかったのですが…
本記事の構成は以下の通りです。
理論
Hard K-means法
K-means法はデータをK個のクラスに分類する手法で、典型的には幾何学的・解析的に解が求まるHard K-means法が扱われます。 標本$\boldsymbol{y}_ 1,\ldots,\boldsymbol{y}_ N$を$K$個のクラスターに分類したいとします。ここで$\boldsymbol{y}_n = (y_{1n},\ldots, y_{Dn})$、変数の数は$D$です。
Hard K-means法では$\boldsymbol{y}_ n $を任意のクラスター$\boldsymbol{Z} = (Z_1,\ldots,Z_N )$, $Z_n ∈ \left(1,\ldots,K\right)$に割り当て、各クラスター平均$\boldsymbol{\mu}_{1},\ldots,\boldsymbol{\mu} _K$、$\boldsymbol{\mu} _k = ( \mu_{1k}, \ldots, \mu_{Dk})$を計算し、各標本との距離の合計$\sum_{n=1}^{N}\sum_{d=1}^{D}\left(y_{dn} - \mu_{dZ_{[n]}}\right)^2$が最小になるような割り当て方法を模索します。結果は一意に定まります。
Soft K-means法
一方、Soft K-means法は$\boldsymbol{y}_n$が各クラスターに含まれる確率が結果として得られます。またユークリッド距離と多変量正規分布の関係から、モデルは多変量正規分布で表現されます。
各標本の割り当て先$Z_n$が以下のカテゴリカル分布に従うとします。
$$
Z_n \sim \mathrm{Categorical}\left(\boldsymbol{\theta}\right) \tag{1}
$$
$$
\boldsymbol{\theta} = \left(\theta_1, \ldots, \theta_K\right), ~~ \sum_{k=1}^{K}\theta_k = 1 \tag{2}
$$
$\boldsymbol{\theta}$は各クラスターに含まれる標本の全体に占める割合とみなせます。
次に、1標本$\boldsymbol{y}_n$は、$Z_n$に割り当てられる場合、次の多変量正規分布に従うものとします。
$$
\boldsymbol{y}_n \sim \mathrm{MultiNormal}\left(\boldsymbol{\mu}_{Z_n}, \Sigma\right) \tag{3}
$$
ここで各変数は互いに独立に生成されるものとすると、
$$ \Sigma = \mathrm{diag[\sigma_1, \ldots, \sigma_D]} \tag{4} $$
となり、このとき$y_{1n},\ldots,y_{Dn}$がそれぞれ独立に平均$\mu_{Z_n}$、標準偏差$\sigma_d$の正規分布に従うことになります。
$\boldsymbol{y}_n$がクラスター$k$に分類されるとき$(Z_n = k)$の対数尤度は、
$$
p_{(Z_n = k)} = \theta_k\mathrm{MultiNormal}(\boldsymbol{y}_n | \boldsymbol{\mu}_{k}, \Sigma) \propto \theta_k \cfrac{1}{\sqrt{\det{\Sigma}}}\exp\left(-\cfrac{1}{2}(\boldsymbol{y}_n - \boldsymbol{\mu}_k)^T\Sigma^{-1}(\boldsymbol{y}_n - \boldsymbol{\mu}_k)\right) = \theta_k\cfrac{1}{\prod_{d=1}^{D}\sigma_d}\exp\left(\sum_{d=1}^{D}\cfrac{1}{2\sigma_d^2}(y_{dn} - \mu_{dk})^2\right) \tag{5}
$$
となります。
$(5)$式にはクラスター平均と標本のユークリッド距離が含まれています。結局Soft K-means法も標本とクラスター中心の距離で結果が決まってくるのですね…$\sigma_d$もおそらく変数間の重みづけ程度の役割なんでしょう。
理論は簡潔にこのくらいで…
実践
サンプルデータの準備
今日は経済産業省から平成26年商業統計500mメッシュデータをダウンロードして利用します。データを集計し、事業所数あたり小売業の総売上と従業員あたり小売業の総売上についての東京都内20km四方1km単位メッシュデータを作成します。中で適宜てきとうに欠損値の置き換えや外れ値の置き換えをしています。
# 読み込みと集計 -----------------------------------------------------------------
library(tidyverse)
d <- read.csv("data(big)/H26_03_500m都道府県.csv", header=F)
# 東京都内の20km×20kmをfilter
d %>% as.data.frame() %>% mutate(mesh2 = paste(!!!rlang::syms(c("V5", "V6")), sep="")) %>% # 2次メッシュコードを作成
filter(mesh2 == 533955 | mesh2 == 533956 | mesh2 == 533945 | mesh2 == 533946 ) %>% # 2次メッシュコードでフィルター
select(mesh2, loc = V7, Office = V22, Employees = V23, Sales = V24) %>% # 必要な列のみ抽出
mutate(rowID = as.numeric(case_when(str_sub(loc,end=-2) == "" ~ "0",TRUE ~ str_sub(loc,end=-2)))) %>% # 2次メッシュ内でのの行番号を作成
mutate(colID = as.numeric(str_sub(loc,start=-1))) %>% # 2次メッシュ内での列番号を作成
mutate(rowID = if_else(mesh2 == 533955 | mesh2 == 533956, rowID + 10, rowID)) %>% # 全体における行番号を作成
mutate(colID = if_else(mesh2 ==533956 | mesh2 == 533946, colID + 10, colID)) %>% # 全体における列番号を作成
na_if("X") %>% mutate_if(is.character, as.numeric) %>% # 欠損値XをNAに置き換える+全部double型に変換
group_by(mesh2, loc) %>% mutate_at(vars(Office, Employees, Sales), list( ~replace_na(.,mean(.,na.rm=TRUE)))) %>% # 3次メッシュでグループ化・NAをグループごとの平均値で置換
ungroup() %>% select(rowID, colID, Sales, Employees, Office ) %>% # 必要な列だけ取り出す
group_by(rowID, colID,) %>% summarise_all(funs(sum(.))) %>% # 3次メッシュで和をとる
ungroup() %>% mutate(SE = Sales / Employees, SO = Sales / Office) %>% # Sales/EmployeesとSales/Officeを計算
mutate_at(vars(SE, SO), ~replace_na(.,mean(.,na.rm=TRUE))) %>% arrange(desc(SE)) -> d
d[1,6] <- d[2,6] # 外れ値を置き換え ridyverseでのうまいやり方がわからぬ
d %>% arrange(desc(SO)) -> d
d[1:3,7] <- d[4,7] # さらに外れ値を置き換え
d %>% select(rowID, colID, SE, SO) -> d
# 描画 ----------------------------------------------------------------------
p <- ggplot(data=d, aes(x=colID, y=rowID, z=SO, fill=SO))
p <- p + theme_bw(base_size=9) + theme(legend.position = "none")
p <- p + theme(panel.background = element_blank()) + theme(legend.title = element_blank()) + theme(panel.grid = element_blank())
p <- p + geom_tile()
p <- p + scale_fill_gradient2(low="white",mid="#A6CEE3", high="#1F78B4")
p <- p + labs(title="Sales/Office")
p <- p + scale_x_continuous(breaks=seq(0,19))
p <- p + scale_y_continuous(breaks=seq(0,19))
p <- p + xlab("") + ylab("")
p <- p + geom_text(aes(label=round(SO,2)), col="grey8",size=2.3)
p2 <- ggplot(data=d, aes(x=colID, y=rowID, z=SE, fill=SE))
p2 <- p2 + theme_bw(base_size=9) + theme(legend.position = "none")
p2 <- p2 + theme(panel.background = element_blank()) + theme(legend.title = element_blank()) + theme(panel.grid = element_blank())
p2 <- p2 + geom_tile()
p2 <- p2 + scale_fill_gradient2(low="white",mid="#A6CEE3", high="#1F78B4")
p2 <- p2 + labs(title="Sales/Office")
p2 <- p2 + scale_x_continuous(breaks=seq(0,19))
p2 <- p2 + scale_y_continuous(breaks=seq(0,19))
p2 <- p2 + xlab("") + ylab("")
p2 <- p2 + geom_text(aes(label=round(SE,2)), col="grey8",size=2.3)
library(gridExtra)
p_extra <- gridExtra::grid.arrange(p,p2, ncol=2)
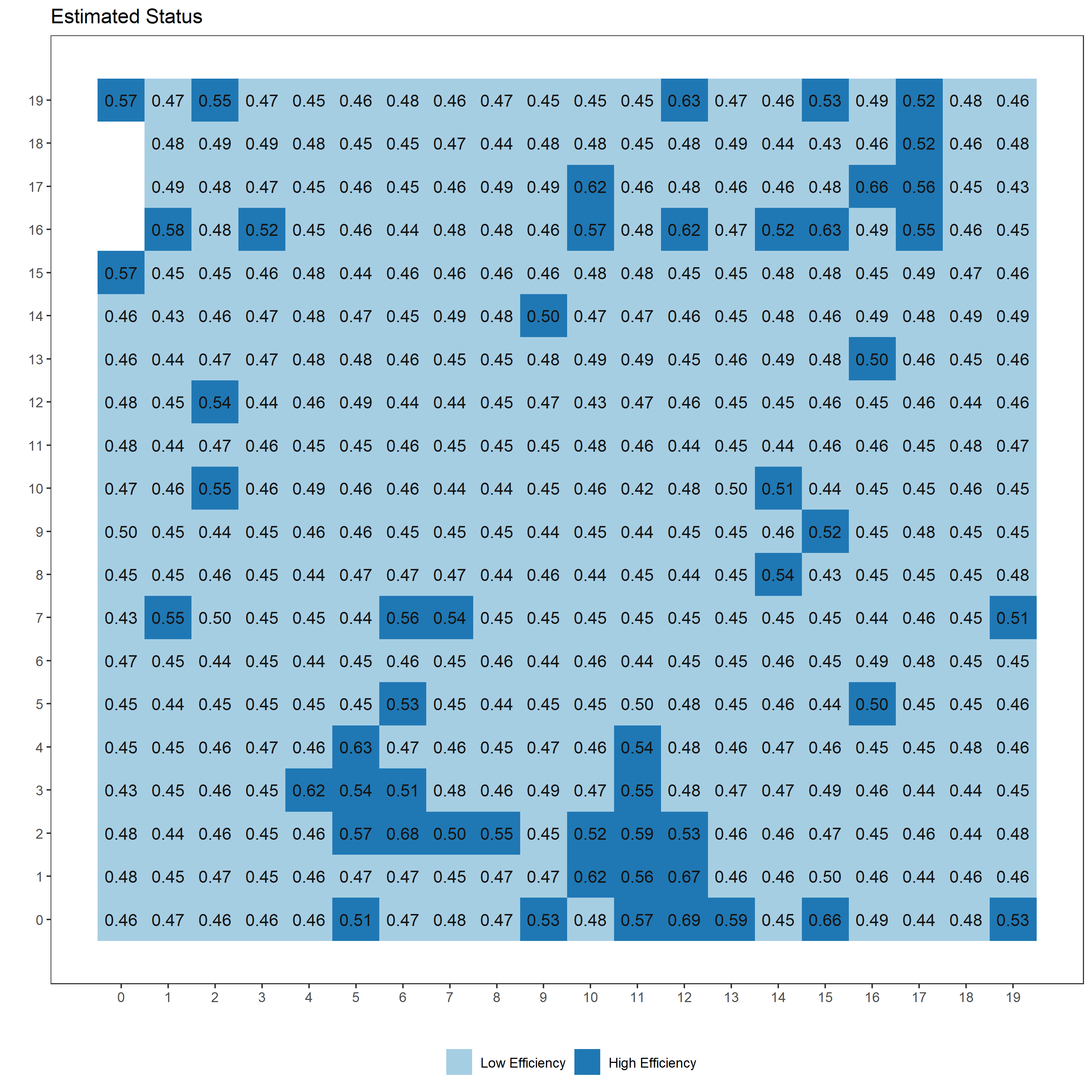
このデータに対してソフトクラスタリングを実行し、事業所ごと・従業員毎の生産性が高い（High Efficiency）地域と低い（Low Efficiency）にメッシュを二分することを目的にします。
実装
実装は基本的に理論編での数式に倣いますが、標準偏差$\sigma_1,\ldots,\sigma_D$はすべて1とします（個人的に$\sigma_k$を軽視しているのと、$\sigma_k$をパラメータにすると収束しなかったため）。
Stanコードは以下です。
//model.stan
data{
int D; //入力数
int N; //サンプル数
int K; //クラス数
vector[D] Z[N]; //外で標準化済み
}
parameters{
simplex[K] theta; //各クラスターへ割り振られる確率
ordered[K] Z_mu[D]; //クラスター平均
}
transformed parameters{
vector<upper=0>[K] soft_z[N]; //クラスター毎の対数尤度
matrix[K,N] dotself = rep_matrix(0,K,N);
for(k in 1:K){
for(n in 1:N){
for(d in 1:D){
dotself[k,n] += (Z_mu[d,k] - Z[n,d])^2;
}
}
}
//クラスター毎の対数尤度の計算
for(n in 1:N){
for(k in 1:K){
soft_z[n,k] = log(theta[k]) - 0.5 * dotself[k,n];
}
}
}
model{
//likelihood
for(n in 1:N){
target += log_sum_exp(soft_z[n]);
}
}
generated quantities{
vector[K] p[N];
for(n in 1:N){
p[n] = softmax(soft_z[n]);
}
}
一つ目のポイントはordered Z_mu[D]でしょうか。ラベルスイッチングと呼ばれる、クラスターを識別できない問題を解消しています。これがないと全く収束しません。
二つ目のポイントはvector<upper=0>[K] soft_z[N]とtarget += log_sum_exp(soft_z[n])ですね。$N$個の$K$ベクトルsoft_zの要素には$(5)$式の対数尤度が格納されています。それを関数log_sum_exp()を使って混合モデルとして認識させtargetに足していきます。詳しくはアヒル本203ページを参照のこと。
三つ目のポイントはp[n] = softmax(soft_z[n])です。ソフトマックス関数について思い出して下さい。
$$
\mathrm{softmax}(\boldsymbol{x}_ n) = \left(\cfrac{\exp(x_{1n})}{\sum_{k=1}^K \exp(x_{kn})}\cdots\cfrac{\exp(x_{Kn})}{\sum_{k=1}^K \exp(x_{kn})} \right) \tag{6}
$$
対数尤度が格納されたsoft_zを$\exp()$で再び尤度に戻しています。尤度比がそのまま各クラスターに分類される確率と解釈できる訳です。
結果
以下でMCMCを走らせ、$\hat{R}$で収束を確認します。
library(rstan)
D <- 2
N <- nrow(d)
loc <- d[,c(1,2)]
Z <- scale(d[,c(3,4)])
K <- 2
rstan_options(auto_write = TRUE)
options(mc.cores = parallel::detectCores())
data <- list(D=D,N=N,Z=Z, K=K)
stanmodel <- stan_model("model.stan")
fit <- sampling(stanmodel, pars = c("Z_mu","theta","p"),
data=data, iter=1300, warmup=300, seed=123, chain=4)
fit
## Inference for Stan model: model.
## 4 chains, each with iter=1300; warmup=300; thin=1;
## post-warmup draws per chain=1000, total post-warmup draws=4000.
##
## mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
## Z_mu[1,1] -0.18 0.00 0.05 -0.28 -0.22 -0.18 -0.15 -0.08 4664 1
## Z_mu[1,2] 2.98 0.00 0.27 2.47 2.79 2.98 3.16 3.54 3989 1
## Z_mu[2,1] -0.19 0.00 0.06 -0.30 -0.23 -0.19 -0.15 -0.09 4715 1
## Z_mu[2,2] 3.19 0.00 0.27 2.68 3.01 3.18 3.36 3.73 4215 1
## theta[1] 0.94 0.00 0.01 0.91 0.93 0.94 0.95 0.97 3832 1
## theta[2] 0.06 0.00 0.01 0.03 0.05 0.06 0.07 0.09 3832 1
## p[1,1] 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 3445 1
## p[1,2] 1.00 0.00 0.00 1.00 1.00 1.00 1.00 1.00 3445 1
## p[2,2] 1.00 0.00 0.00 1.00 1.00 1.00 1.00 1.00 3633 1
## p[2,1] 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 3633 1
～以下省略～
結果はざっとこんな感じです。
# 分類結果を描画するRスクリプト ---------------------------------------------------------
fit %>% rstan::extract() %>% as.data.frame() %>% select(starts_with("p")) %>% select(ends_with("2")) %>% # 2で終わるpがhighである確率に対応。MCMCサンプルから抽出
pivot_longer(everything(), names_to = "key", values_to = "val") %>% # 縦持ち型に変換
mutate(loc=str_sub(str_sub(key, start=3),end=-3), key=NULL) %>% # keyから位置のID(loc)を抽出
group_by(loc) %>% summarise(median=median(val), lower=quantile(val, 0.25), upper=quantile(val,0.75)) %>%
mutate(Class = as.factor(round(median))) %>% merge(cbind(loc=seq(1,nrow(d)),d), by="loc") %>% select(-loc) -> res_data
library(ggplot2)
color1 <- colorRampPalette(c("#A6CEE3","#1F78B4"))
p <- ggplot()
p <- p + theme_bw(base_size=11)
p <- p + theme(panel.background = element_blank()) + theme(legend.title = element_blank()) + theme(panel.grid = element_blank())+
theme(legend.position = "bottom")
p <- p + scale_y_continuous(breaks=seq(0,19))
p <- p + geom_tile(data=data.frame(res_data), aes(x=colID, y=rowID, fill=Class))+
scale_fill_hue(palette=color1, breaks=c("0", "1"),labels=c("Low Efficiency", "High Efficiency"))
p <- p + geom_text(data=data.frame(res_data), aes(x=colID, y=rowID, label=sprintf("%0.2f", median)), colour = "grey8")
p <- p + xlab("") + ylab("")
p <- p + scale_x_continuous(breaks=seq(0,19))
p <- p + labs(title="Estimated Status")
# パラメータや生成量の事後分布を描画 -------------------------------------------------------
library(bayesplot)
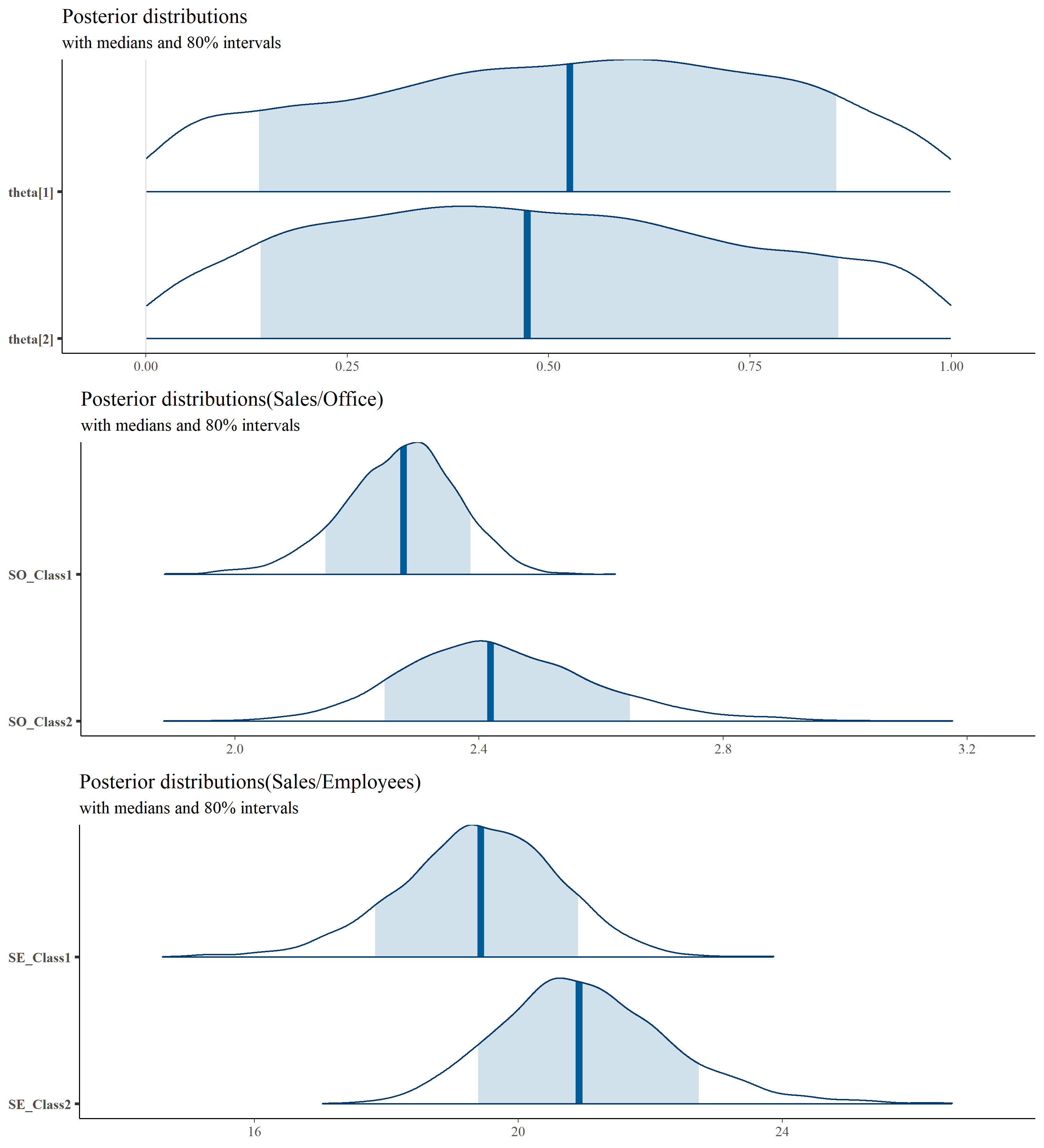
plot_title <- ggtitle("Posterior distributions",
"with medians and 80% intervals")
posterior <- as.matrix(fit)
colnames(posterior)[which(colnames(posterior)=="Z_mu[1,1]")] <- "SO_Class1_normalize" # Sales/Office
colnames(posterior)[which(colnames(posterior)=="Z_mu[1,2]")] <- "SO_Class2_normalize"
colnames(posterior)[which(colnames(posterior)=="Z_mu[2,1]")] <- "SE_Class1_normalize" # Sales/Employees
colnames(posterior)[which(colnames(posterior)=="Z_mu[2,2]")] <- "SE_Class2_normalize"
# 標準化したSales/OfficeとSales/Employeesをもとに戻す
posterior %>% as.data.frame() %>%
mutate(SO_Class1 = SO_Class1_normalize * attr(Z,'scaled:scale')[1] + attr(Z, 'scaled:center')[1],
SO_Class2 = SO_Class2_normalize * attr(Z, 'scaled:center')[1] + attr(Z, 'scaled:center')[1],
SE_Class1 = SE_Class1_normalize * attr(Z, 'scaled:center')[2] + attr(Z, 'scaled:center')[2],
SE_Class2 = SE_Class2_normalize * attr(Z, 'scaled:center')[2] + attr(Z, 'scaled:center')[2],
SO_Class1_normalize = NULL,
SO_Class2_normalize = NULL,
SE_Class1_normalize = NULL,
SE_Class2_normalize = NULL,
sigma=NULL) -> posterior
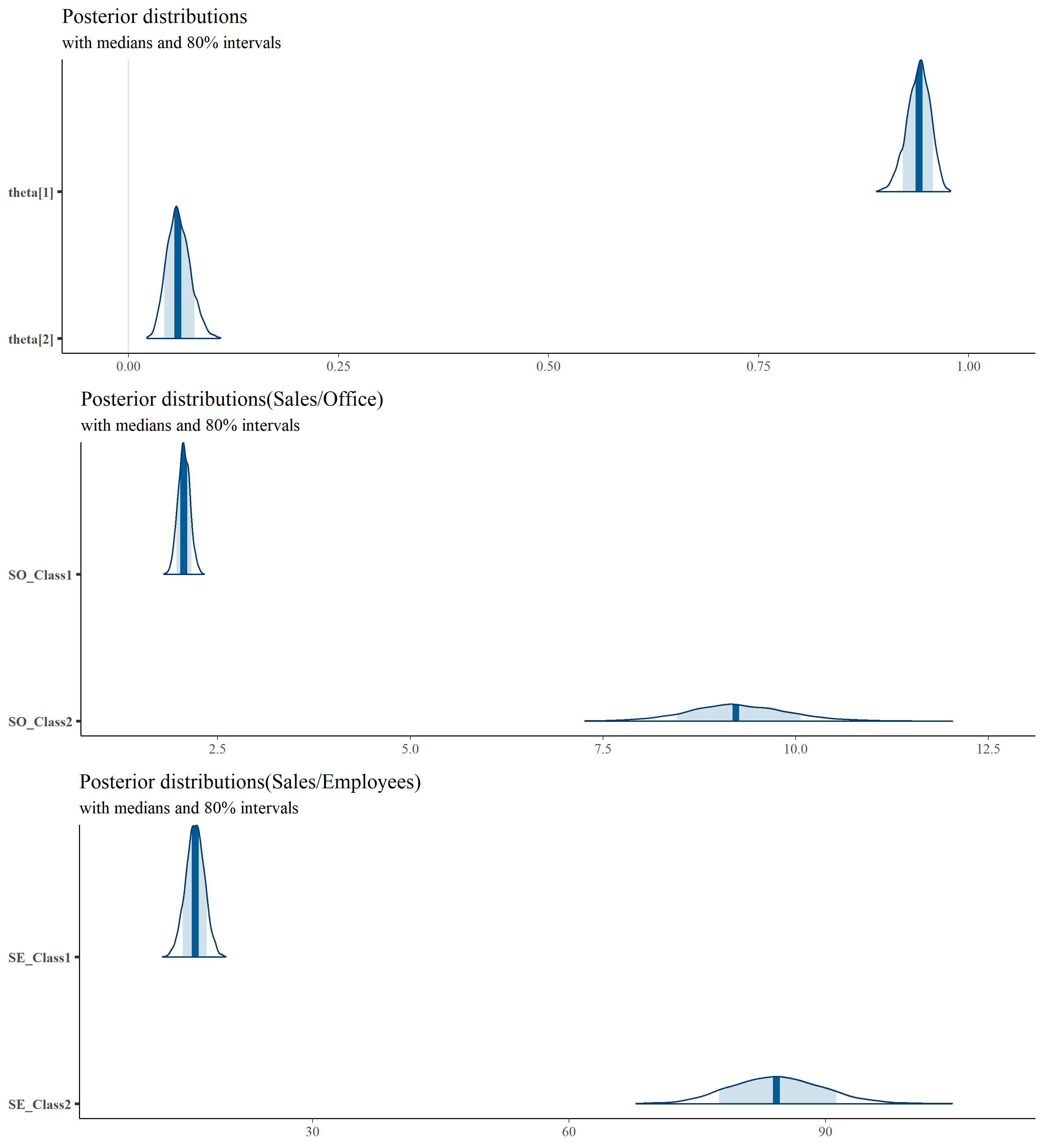
plot1 <- mcmc_areas(posterior,
regex_pars = c("sigma", "theta"),
prob = 0.8) + plot_title
plot2 <- mcmc_areas(posterior,
pars = c("SO_Class1","SO_Class2"), prob=0.8) +
ggtitle("Posterior distributions(Sales/Office)",
"with medians and 80% intervals")
plot3 <- mcmc_areas(posterior,
pars = c("SE_Class1","SE_Class2"), prob=0.8) +
ggtitle("Posterior distributions(Sales/Employees)",
"with medians and 80% intervals")
p_extra <- gridExtra::grid.arrange(plot1,plot2,plot3, ncol=1)
# 推定した混合正規分布の確率密度を描画 ------------------------------------------------------
posterior <- as.data.frame(fit)
colnames(posterior)[which(colnames(posterior)=="Z_mu[1,1]")] <- "SO_Class1_normalize" # Sales/Office
colnames(posterior)[which(colnames(posterior)=="Z_mu[1,2]")] <- "SO_Class2_normalize"
colnames(posterior)[which(colnames(posterior)=="Z_mu[2,1]")] <- "SE_Class1_normalize" # Sales/Employees
colnames(posterior)[which(colnames(posterior)=="Z_mu[2,2]")] <- "SE_Class2_normalize"
posterior %>% select(-starts_with(c("p","lp__"))) %>%
mutate(SO_Class1 = SO_Class1_normalize * attr(Z,'scaled:scale')[1] + attr(Z, 'scaled:center')[1],
SO_Class2 = SO_Class2_normalize * attr(Z, 'scaled:center')[1] + attr(Z, 'scaled:center')[1],
SE_Class1 = SE_Class1_normalize * attr(Z, 'scaled:center')[2] + attr(Z, 'scaled:center')[2],
SE_Class2 = SE_Class2_normalize * attr(Z, 'scaled:center')[2] + attr(Z, 'scaled:center')[2],
sigma_SO = 1 * attr(Z,'scaled:scale')[1],
sigma_SE = 1 * attr(Z,'scaled:scale')[2]) %>%
select(SO_Class1, SO_Class2, SE_Class1, SE_Class2, sigma_SO, sigma_SE, starts_with("theta") )-> res_data
# 混合正規分布の確率密度関数を作成。中央値を用いる
bw1 <- diff(range(d[,3]))/30
bw2 <- diff(range(d[,4]))/30
dmixnorm1 <- function(x) bw1 * nrow(d) *median(res_data$'theta[1]') * dnorm(x,mean=median(res_data$SO_Class1), sd=median(res_data$sigma_SO)) +
bw1 * nrow(d) * median(res_data$'theta[2]') * dnorm(x,mean=median(res_data$SO_Class2), sd=median(res_data$sigma_SO))
dmixnorm2 <- function(x) bw2 * nrow(d) * median(res_data$'theta[1]') * dnorm(x,mean=median(res_data$SE_Class1), sd=median(res_data$sigma_SE)) +
bw2 * nrow(d) * median(res_data$'theta[2]') * dnorm(x,mean=median(res_data$SE_Class2), sd=median(res_data$sigma_SE))
dmixnorm1_samples <- function(x, sample) bw1 * nrow(d) *res_data$'theta[1]'[sample] * dnorm(x,mean=res_data$SO_Class1[sample], sd=res_data$sigma_SO[sample]) +
bw1 * nrow(d) * res_data$'theta[2]'[sample] * dnorm(x,mean=res_data$SO_Class2[sample], sd=res_data$sigma_SO[sample])
dmixnorm2_samples <- function(x, sample) bw2 * nrow(d) * res_data$'theta[1]'[sample] * dnorm(x,mean=res_data$SE_Class1[sample], sd=res_data$sigma_SE[sample]) +
bw2 * nrow(d) * res_data$'theta[2]'[sample] * dnorm(x,mean=res_data$SE_Class2[sample], sd=res_data$sigma_SE[sample])
# 雲を纏わせる
samples <- sample(seq(1,4000), size=80, replace=FALSE)
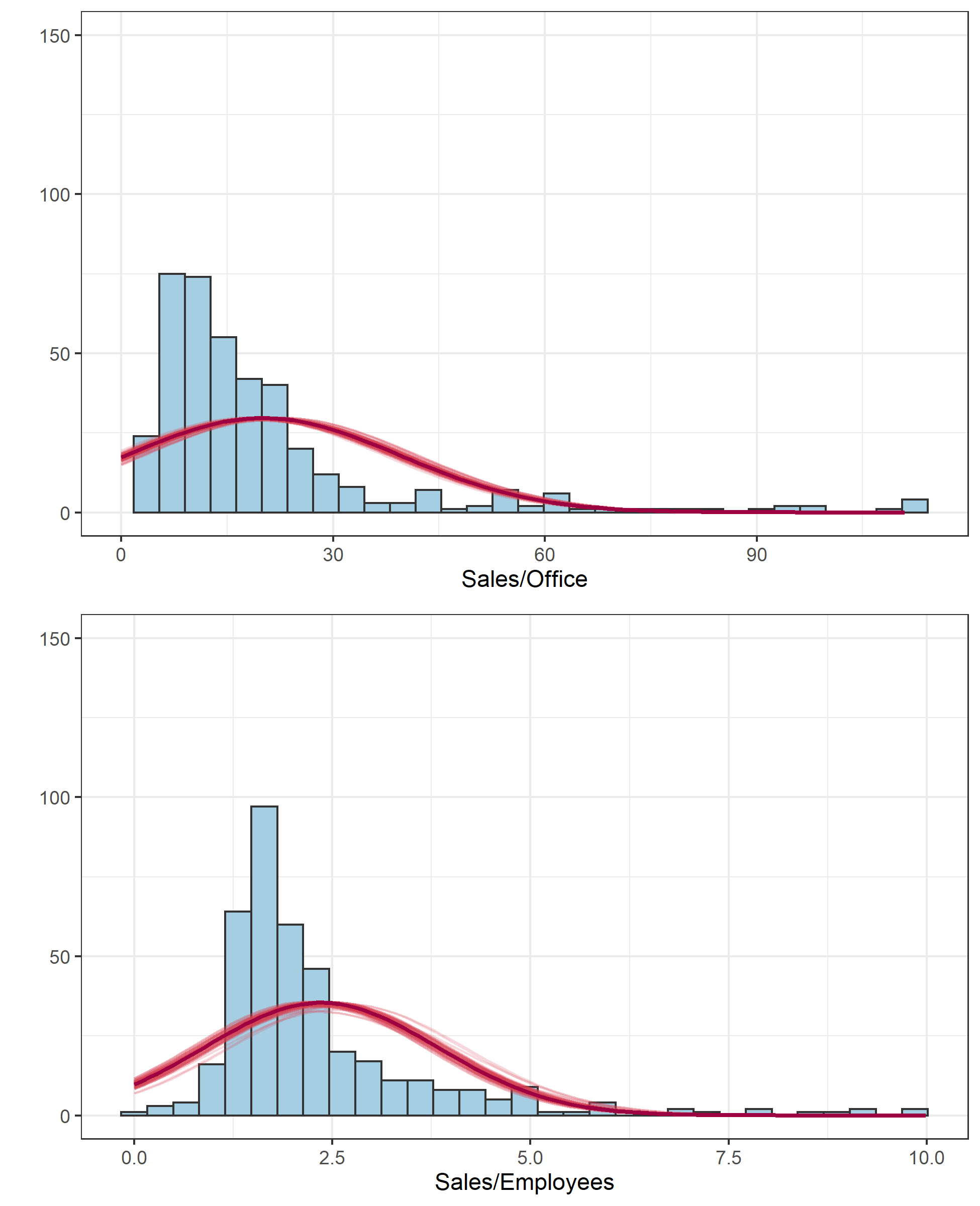
q1 <- ggplot(data=d[,3],aes(x=SE))
q1 <- q1 + theme_bw(base_size=11)
q1 <- q1 + geom_histogram(binwidth = bw1, fill="#A6CEE3", color = "grey20")
for(n in 1:length(samples)){
q1 <- q1 + stat_function(fun=dmixnorm1_samples, args=list(sample=samples[n]), color = "#D53E4F", alpha=0.2, size = 0.5, xlim=c(0, max(d[,3])))
}
q1 <- q1 + stat_function(fun=dmixnorm1, color = "#9E0142", size = 1, xlim=c(0, max(d[,3])))
q1 <- q1 + xlab("Sales/Employees") + ylab("")
q1 <- q1 + coord_cartesian(ylim=c(0,150))
q2 <- ggplot(data=data.frame(x=d[,4]),aes(x=SO))
q2 <- q2 + theme_bw(base_size=11)
q2 <- q2 + geom_histogram(binwidth = bw2, fill="#A6CEE3", color = "grey20") +labs("aa")
for(n in 1:length(samples)){
q2 <- q2 + stat_function(fun=dmixnorm2_samples, args=list(sample=samples[n]), color = "#D53E4F", alpha=0.2, size = 0.5, xlim = c(0,max(d[,4])))
}
q2 <- q2 + stat_function(fun=dmixnorm2, color = "#9E0142", size = 1, xlim = c(0,max(d[,4])))
q2 <- q2 + xlab("Sales/Office") + ylab("")
q2 <- q2 + coord_cartesian(ylim=c(0,150))
q <- gridExtra::grid.arrange(q2,q1,ncol = 1)
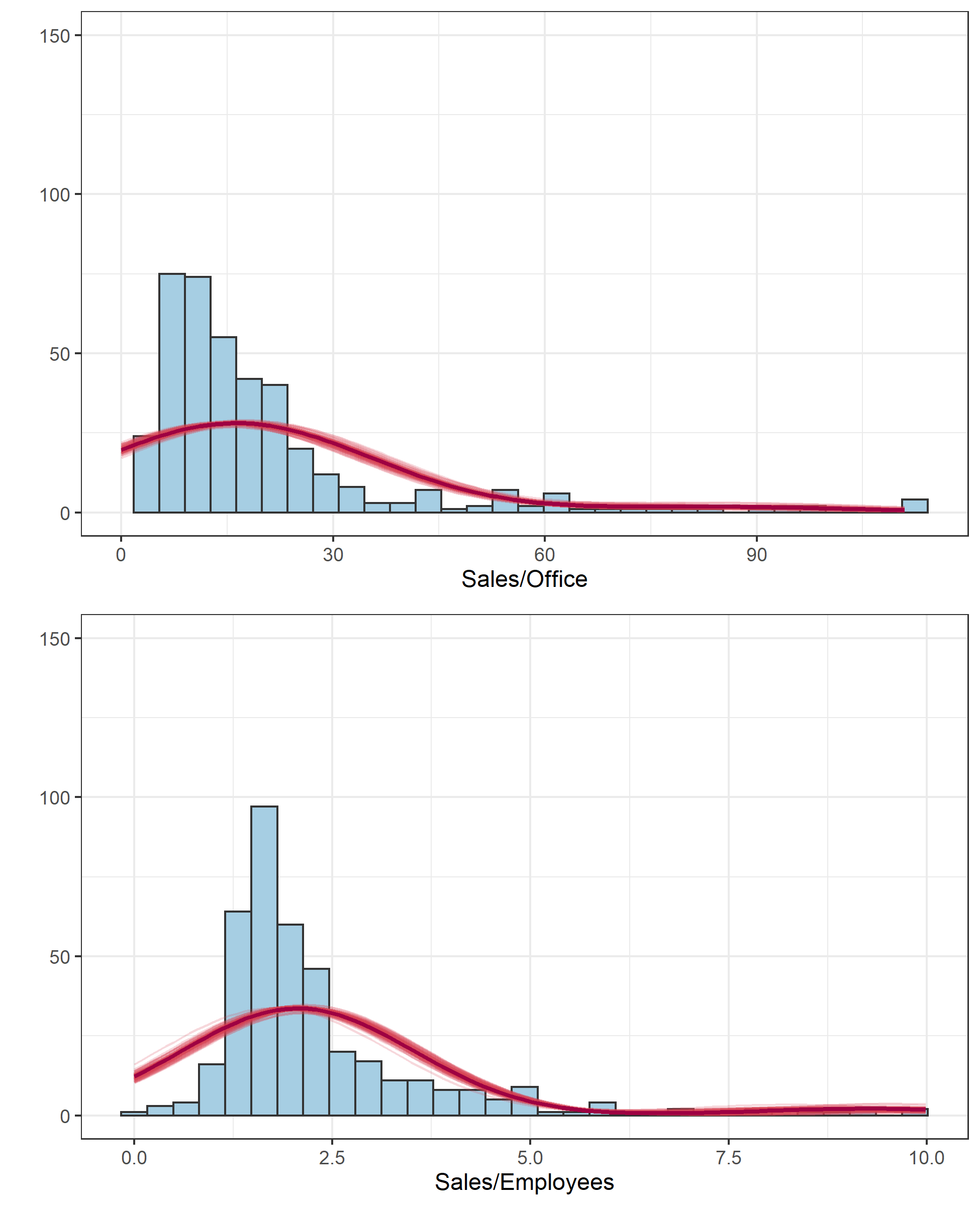
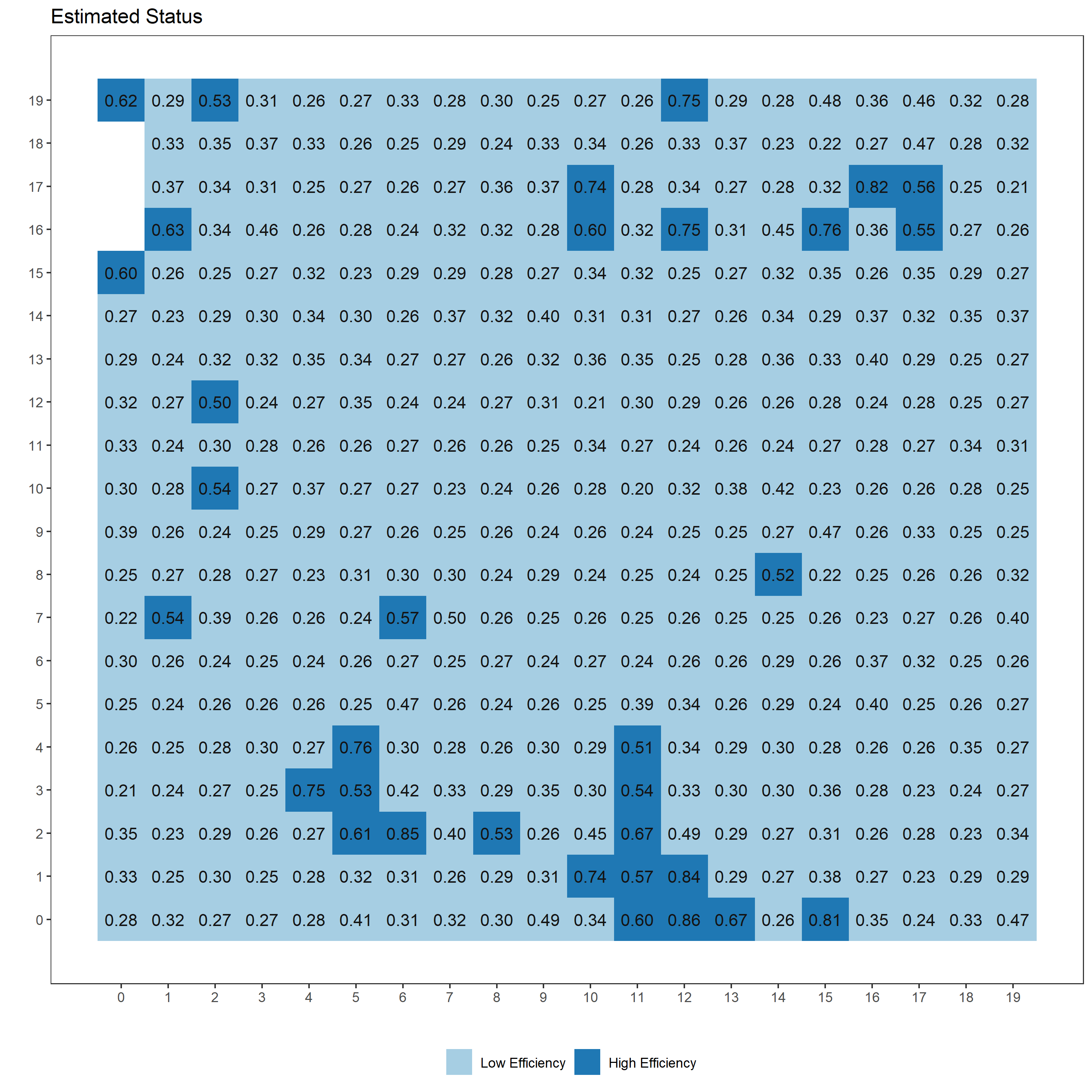
無難な結果が得られているのではないかなあ、という感じです。はじめのタイル図がクラスタリングの推定結果ですが、タイルごとに「High Efficiency」である確率の事後分布の中央値を示しています。このように各クラスターへ分類される確率で結果が得られるのがSoft K-means法の特徴です。
ガウス過程をあてはめてみる
問題はここからです。ただクラスタリングを試すだけなら空間データを扱う必要はありません。なぜ今回空間データを扱ったかというと、普遍的なモデルにガウス過程を組み込む練習がしたかったからです。
ガウス過程は「近い距離関係にある変数同士ほど近い値をとる」というような性質を変数間に与えることが可能です。今回は文字通り地理的に近い距離関係にある地域ほど小売業の「Efficiency」は近い値をとるだろう、という関係をガウス過程を使って上記モデルに組み込んでみたいと思います1。
追加する計算は以下のとおりです。
$$
\mathrm{logit}(\boldsymbol{p}_{(Z_n = k)}) \sim \mathrm{MultiNormal}(\boldsymbol{0}_n, K) \tag{7}
$$
$$
\boldsymbol{p}_{(Z_n = k)} = (p_{Z_1=k},\ldots,p_{Z_n=k})^T, ~~~ \boldsymbol{0}_n = (0,\ldots,0)^T∈\mathbb{R}^n \tag{8}
$$
$$
k_{nn'} = \phi_{\boldsymbol{loc}_n}^T\phi_{\boldsymbol{loc}_{n'}} \tag{9}
$$
$\mathrm{logit}(\boldsymbol{p}_ {(Z_ n = k)})$の各要素の平均値を0としているので、各クラスが「High Efficiency」である確率は情報に乏しい付近では0.5に収束するようなガウス過程です。 ここで$k_{nn’}$はグラム行列$K$の$(n,n’)$成分です。$\boldsymbol{loc}_n$には$n$番目の変数の座標$(x,y)$が格納されています。$\phi$はカーネル関数です。今回はガウスカーネルを使ってみます。
上記モデルの実装は以下です。以前の記事でガウス過程のいパーパラメータ推定は懲りたので、今回はこちらからハイパーパラメータを指定していきます。
//model2.stan
data{
int D; //入力数
int N; //サンプル数
int K; //クラス数
vector[2] loc[N]; //入力位置
vector[D] Z[N];
real alpha;
real rho;
real delta_sq;
}
transformed data{
vector[N] Mu;
for(i in 1:N) Mu[i] = 0;
}
parameters{
simplex[K] theta; //各クラスターへ割り振られる確率
ordered[K] Z_mu[D]; //クラスター平均
}
transformed parameters{
vector<upper=0>[K] soft_z[N]; //クラスター毎の対数尤度
vector[K] p[N];
matrix[N,K] p_logit; //matrix型なら列・行どちらの取り出しでもベクトル型になる
matrix[K,N] dotself = rep_matrix(0,K,N);
matrix[N,N] cov;
for(k in 1:K){
for(n in 1:N){
for(d in 1:D){
dotself[k,n] += (Z_mu[d,k] - Z[n,d])^2;
}
}
}
//クラスター毎の対数尤度の計算
for(n in 1:N){
for(k in 1:K){
soft_z[n,k] = log(theta[k]) - 0.5 * dotself[k,n];
}
}
for(n in 1:N){
p[n] = softmax(soft_z[n]);
p_logit[n,] = logit(p[n])';
}
// カーネル行列の作成
cov = cov_exp_quad(loc, alpha, rho);
for(n in 1:N){
cov[n,n] = cov[n,n] + delta_sq;
}
}
model{
//likelihood
for(n in 1:N){
target += log_sum_exp(soft_z[n]);
}
//GP
for(k in 1:(K-1)){
p_logit[,k] ~ multi_normal(Mu, cov);
}
}
以下で上記モデルを走らせ、結果を確認します。ハイパーパラメータは$\alpha=30$、$\rho=1.15$で。
data <- list(D=D,N=N,Z=Z,loc=loc,alpha=30, rho=1.15, delta_sq=0.01, K=K)
stanmodel2 <- stan_model("model2.stan")
fit2 <-sampling(stanmodel2, pars = c("Z_mu","theta","p"),
data=data, iter=1300, warmup=300, seed=123)
fit2
## Inference for Stan model: model2.
## 4 chains, each with iter=1300; warmup=300; thin=1;
## post-warmup draws per chain=1000, total post-warmup draws=4000.
##
## mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
## Z_mu[1,1] -0.11 0.00 0.06 -0.24 -0.15 -0.11 -0.07 0.01 1781 1.00
## Z_mu[1,2] 0.48 0.01 0.17 0.10 0.38 0.49 0.60 0.80 978 1.00
## Z_mu[2,2] 0.46 0.01 0.17 0.09 0.36 0.47 0.58 0.77 783 1.00
## Z_mu[2,1] -0.11 0.00 0.06 -0.23 -0.15 -0.11 -0.07 0.01 2398 1.00
## theta[1] 0.80 0.00 0.09 0.55 0.77 0.82 0.85 0.90 553 1.01
## theta[2] 0.20 0.00 0.09 0.10 0.15 0.18 0.23 0.45 553 1.01
## p[1,1] 0.03 0.00 0.06 0.00 0.01 0.01 0.03 0.18 593 1.00
## p[1,2] 0.97 0.00 0.06 0.82 0.97 0.99 0.99 1.00 593 1.00
## p[2,1] 0.04 0.00 0.06 0.00 0.01 0.02 0.04 0.20 599 1.00
## p[2,2] 0.96 0.00 0.06 0.80 0.96 0.98 0.99 1.00 599 1.00
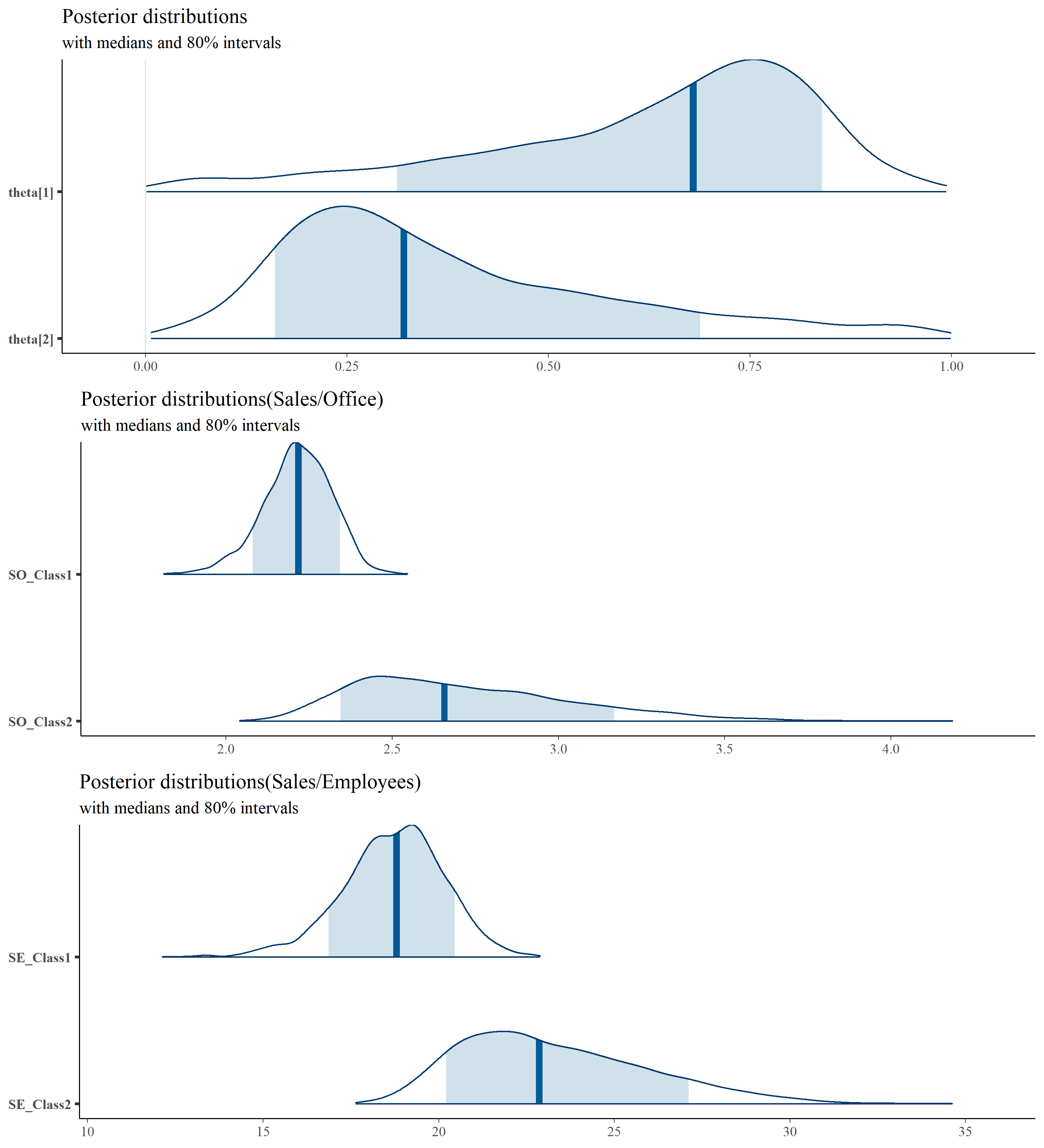
ん、確かに確率が空間的に滑らかにつながったように見えなくもないが、依然として隣り合ったセル間の差が大きいところもあるな… $\rho$を微妙に大きく1.2にして、いびつさをもう少し和らげたガウス過程にしてみよう。
data <- list(D=D,N=N,Z=Z,loc=loc,alpha=30, rho=1.2, delta_sq=0.01, K=K)
fit2 <-sampling(stanmodel2, pars = c("Z_mu","theta","p"),
data=data, iter=1300, warmup=300, seed=123)
(以降、省略)
ハイパーパラメータの値を少しだけ変えただけなのに、今度は手のひらを返したかのように優柔不断な分類結果が得られてしまった。どのセルも確率がほぼ0.5ではないか。
もっと、クラスター平均がある程度離れたまま、空間的に滑らかで急な変化の少ない確率群が得られるかと予想していたのだが…
はじめは実装に問題があるのかと思ったのですが、組み立てたモデルの動作を想像すると原因がすぐにわかりました。
$\rho$をある程度大きくしてなだらかな曲線を描くガウス過程にすると、まず「High Efficiency」だろうと言えるセルのとなりの「Low Efficiecy」っぽいセルまでもが、「High Efficiency」であるという確率が高くなってしまい、その結果二つのクラスターの平均値が近づいて行ってしまうようです。
組み立てたモデルがうまくいかないとき、つい実装が悪いのではと疑ってしまいますが、そもそも組み立てたモデルが自分の意図したとおりに動くものなのか、ということを再確認することも大切なんだなと思いました。
-
本当は空間的自己相関を確認してからこういうモデルを検討すべきなのでしょうが、空間的自己相関の知識がまだ中途半端なのでここでは割愛します ↩︎
