本記事では、前回の記事で失敗に終わった相関係数の検定を、レプリカ交換法を使って解決していきたいと思います。
レプリカ交換法の部分は、松浦健太郎氏が運営されていたはてなブログに掲載されていたコードを流用しています。今現在そのブログが見当たらないですが、こちらのスライドでその内容が確認できるようです。
レプリカ交換法自体の詳細な説明は省きます。イメージは、MCMCサンプルを抽出するメインのchainとは別に、複数のchainを用意しておき、さらにそれらのchainでは対数尤度の変化が通常よりも小さく設定されており、値の移動が柔軟に(ランダムにより近く)なっていると。そして、時々メインのchainとその他のchainを交換することで、対数尤度が極端に小さくなる範囲があっても、それをMCMCが越えられるように工夫したMCMC法になっています。
前回、相関の検定で帰無仮説を $$ H_{0_1}: \rho=0 $$ 、対立仮説を $$ H_{1_3}: \rho < -0.3 ~~~~ 0.3 < \rho $$
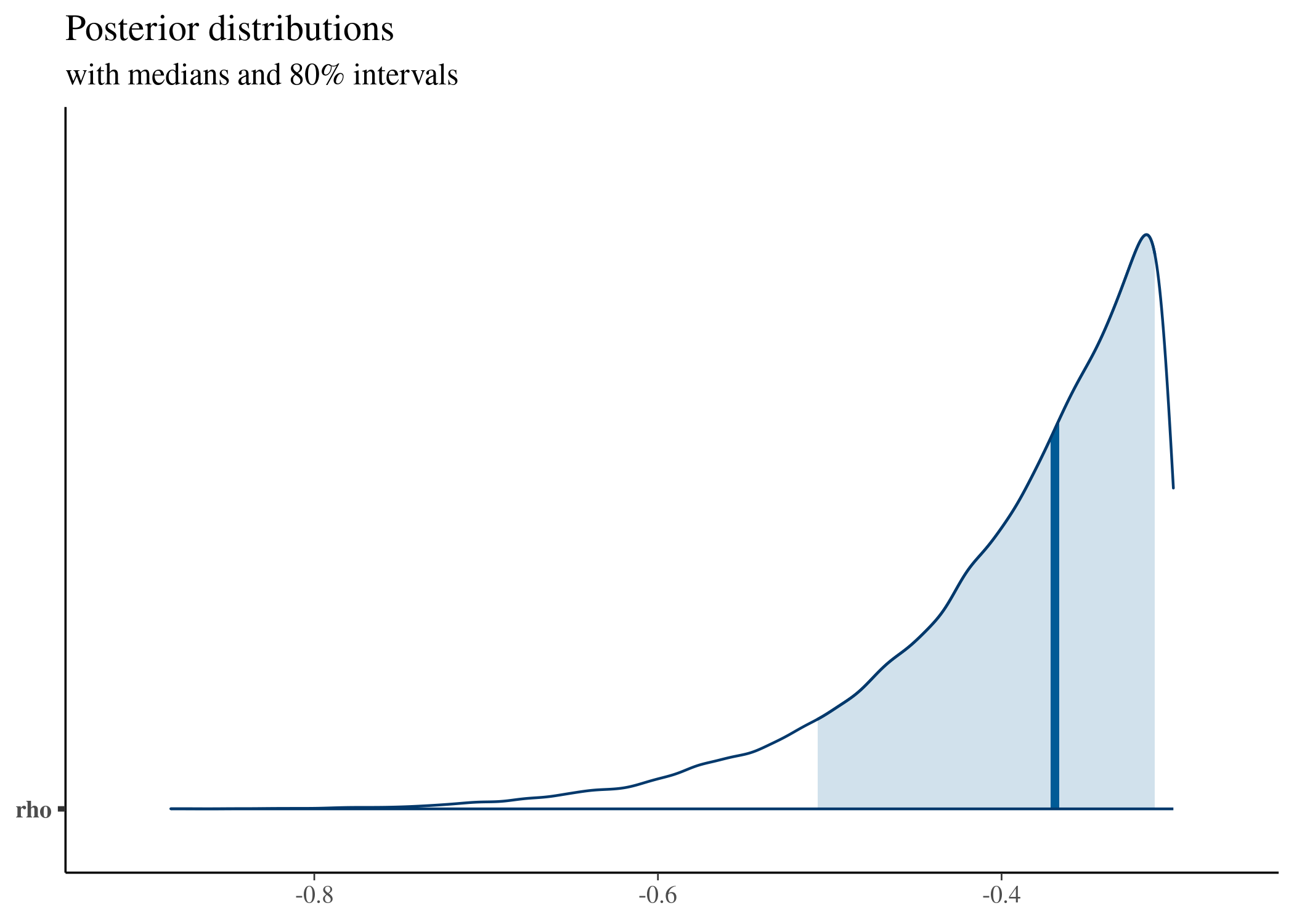
としたとき、実際のデータは$\rho = 0.75$あたりが正解にもかかわらず、初期値をマイナスにすると以下のMCMCサンプルがえられたことから、 $-0.3$から$0.3$の間の対数尤度$-∞$のエリアをMCMCchainが越えられなかったこと失敗の原因があったと伺えます。
まずは、レプリカ交換法を実行する関数を定義していきます。
replica.exchange.mcmc <- function (inv_T, n_ex, stanmodel, data, par_list, init, iter, warmup) {
n_rep <- length(inv_T)
len <- iter - warmup
n_param <- sum(unlist(lapply(par_list, prod))) + 2 # number of parameters included E and lp__
ms_T1 <- matrix(0, len*n_ex, n_param) # MCMC samples at inv_T=1
idx_tbl <- matrix(0, n_ex, n_rep) # index table of (exchange time, replica)
E_tbl <- matrix(0, n_ex, n_rep) # E table along idx_tbl
init_list <- rep(list(init), n_rep)
idx4ex <- function (n_rep, e) if (e %% 2 == 0) 1:floor(n_rep/2) * 2 - 1 else 1:(floor(n_rep/2)-1) * 2
pb <- txtProgressBar(min=1, max=n_ex, style=3)
for (e in seq_len(n_ex)) {
setTxtProgressBar(pb, e)
fit_list <- foreach(r=seq_len(n_rep), .packages='rstan') %dopar% {
data$Inv_T <- inv_T[r]
sampling(
stanmodel, data=data, pars=c(names(par_list), 'E'), init=list(init_list[[r]]),
iter=iter, warmup=warmup, chains=1, seed=r, refresh=-1
)
}
ms_T1[((e-1)*len+1):(e*len), ] <- extract(fit_list[[1]], permuted=FALSE, inc_warmup=FALSE)[,1,]
# exchange replicas
E <- sapply(1:n_rep, function(r) extract(fit_list[[r]], permuted=FALSE, pars='E')[len,1,])
idx <- 1:n_rep
for (r in idx4ex(n_rep, e)) {
w <- exp((inv_T[r] - inv_T[r+1]) * (E[r] - E[r+1]))
if (runif(1,0,1) < w) {
idx[r] <- r+1
idx[r+1] <- r
}
}
E_tbl[e,] <- E
idx_tbl[e,] <- idx
# update init_list
init_list <- lapply(seq_len(n_rep), function(r) {
ms <- extract(fit_list[[idx_tbl[e,r]]], permuted=FALSE, pars=names(par_list))[len,1,]
init <- lapply(names(par_list), function(p) {
pos <- grep(paste0('^', p, '(\\[.*\\])?$'), names(ms))
if (identical(par_list[[p]], 1)) unname(ms[pos]) else array(ms[pos], dim=par_list[[p]])
})
names(init) <- names(par_list)
init
})
}
colnames(ms_T1) <- names(fit_list[[1]])
return(list(ms_T1=ms_T1, idx_tbl=idx_tbl, E_tbl=E_tbl))
}
次に、レプリカ交換法のベースとなるStanコードです。現状では、cmdstanではうまくレプリカ交換法を実行できなかったので、rsta::stan()を使って実行することを想定してコードを書きます。
functions{
real stretched_symmetric_beta_lpdf(real y, real kappa, real lower_rho, real upper_rho, int model_type){
if(model_type == 0)
if( y >= lower_rho && y <= upper_rho )
return
-log(inc_beta(1/kappa, 1/kappa, 0.5 * (upper_rho + 1)) - inc_beta(1/kappa, 1/kappa, 0.5 * (lower_rho + 1))) +
((kappa-2)/kappa) * log(2) - lbeta(1/kappa, 1/kappa) + ((1-kappa)/kappa) * log((1 - square(y)));
else
return negative_infinity();
if(model_type == 1)
if( y <= lower_rho || y >= upper_rho )
return
-log(1 - inc_beta(1/kappa, 1/kappa, 0.5 * (upper_rho + 1)) + inc_beta(1/kappa, 1/kappa, 0.5 * (lower_rho + 1))) +
((kappa-2)/kappa) * log(2) - lbeta(1/kappa, 1/kappa) + ((1-kappa)/kappa) * log((1 - square(y)));
else
return negative_infinity();
else
return negative_infinity();
}
}
data {
int<lower=0> N; // sample size
vector[2] D[N]; // Data consists of X and Y
real kappa;
real Jeffreys_alpha;
real Jeffreys_beta;
real<lower=-1, upper=1> lower_rho;
real<lower=-1, upper=1> upper_rho;
int model_type;
real Inv_T;
//kappa : prior scale of rho
//Jeffreys_alpha : mean of prior(sigma^2) (sufficiently small values)
//Jeffreys_beta : variance of prior(sigma^2) (sufficiently small values)
//model_type
}
parameters {
real<lower=0> sigma_X;
real<lower=0> sigma_Y;
real<lower=-1, upper=1> rho;
vector[2] mu;
// mu consists of mu_X, mu_Y
// mu_X, mu_Y : mean of X and Y, respecttively
// sigma_X, sigma_Y : standard deviation of X and Y, respectively
// rho : correlation of X and Y
}
transformed parameters{
matrix[2,2] cov;
real E;
cov[1,1] = square(sigma_X);
cov[1,2] = sigma_X * sigma_Y * rho;
cov[2,1] = sigma_X * sigma_Y * rho;
cov[2,2] = square(sigma_Y);
{
E = 0;
for (n in 1:N){
E = E - multi_normal_lpdf(D[n] | mu, cov);
}
E = E - stretched_symmetric_beta_lpdf(rho | kappa, lower_rho, upper_rho, model_type);
E = E - gamma_lpdf(square(sigma_X) | Jeffreys_alpha, Jeffreys_beta);
E = E - gamma_lpdf(square(sigma_Y) | Jeffreys_alpha, Jeffreys_beta);
E = E - normal_lpdf(mu | 0, 100);
}
}
model {
target += -Inv_T * E;
}
これらを使って、レプリカ交換法を実行します。はじめに定義しているlog_density()関数は、後で自由エネルギーの計算に使う対数尤度関数です。今回、レプリカ交換法を使う理由でStanファイルをbridge_sampler()に引数として指定することができません。かわりにbridge_sampler()関数にはMCMCサンプルの行列と対数尤度関数、そして各パラメーターの定義域を指定するためのベクトルを与えてやれば自由エネルギーを計算するオプションがついているので、これを使用しています。
log_density <- function(samples.row, data) {
lp <- c()
lp <- stretched_symmetric_beta_lpdf(y=samples.row[3], kappa=kappa, lower_rho = lower_rho,
upper_rho = upper_rho, model_type = model_type) +
dgamma(x = samples.row[1]^2, shape = Jeffreys_alpha, scale = 1 / Jeffreys_beta, log=TRUE ) +
dgamma(x = samples.row[2]^2, shape = Jeffreys_alpha, scale = 1 / Jeffreys_beta, log=TRUE ) +
dnorm(x = samples.row[4], mean = 0, sd = 100, log = TRUE) +
dnorm(x = samples.row[5], mean = 0, sd = 100, log = TRUE)
for(n in 1:nrow(data)){
lp <- lp + dmvnorm(x = data[n,], mean = samples.row[4:5], sigma = matrix(c(samples.row[1]^2,samples.row[1]*samples.row[2]*samples.row[3],samples.row[1]*samples.row[2]*samples.row[3],samples.row[2]^2), nrow=2, ncol=2),
log = TRUE)
}
return(lp)
}
library(doParallel)
library(rstan)
model_informative_rstan <- rstan::stan_model(file=paste0(getwd(),"/model/model_informative_E.stan"))
kappa <- 3
Jeffreys_alpha <- 1e-5
Jeffreys_beta <- 1e-5
# Informative2
lower_rho <- -0.3
upper_rho <- 0.3
model_type <- 1
init <- list(rho = -0.5)
N_rep <- 10 # number of replicas
N_ex <- 100 # number of exchanges
Inv_T <- 0.5^seq(0, -log(0.02)/log(2), len=N_rep)
data_informative <- list(D = d, N = nrow(d), Jeffreys_alpha=Jeffreys_alpha, Jeffreys_beta=Jeffreys_beta,
upper_rho = upper_rho, lower_rho= lower_rho, kappa=kappa, model_type=model_type)
registerDoParallel(detectCores())
res <- replica.exchange.mcmc(inv_T=Inv_T, n_ex=N_ex,
stanmodel = model_informative_rstan, data=data_informative, par_list=list(sigma_X=1, sigma_Y=1, rho=1, mu=2), init=init, iter=600, warmup=100)
# Matrixを使ったBridgesampling
library(zipfR)
library(mvtnorm)
posterior <- as.matrix(res$ms_T1)[10000:nrow(res$ms_T1),1:5]
lb <- c(0,0,-1,-Inf,-Inf)
ub <- c(Inf,Inf,1,Inf,Inf)
names(lb) <- names(ub) <- colnames(posterior)
free_energy_alt <-
bridgesampling::bridge_sampler(samples = posterior, log_posterior = log_density,
lb = lb, ub = ub, data=d)$logml
exp(free_energy_alt - free_energy_null)
# [1] 3.38101
計算の結果推定されたベイズファクターは、
$$ BF_{10_3} ≒ 3.38 $$
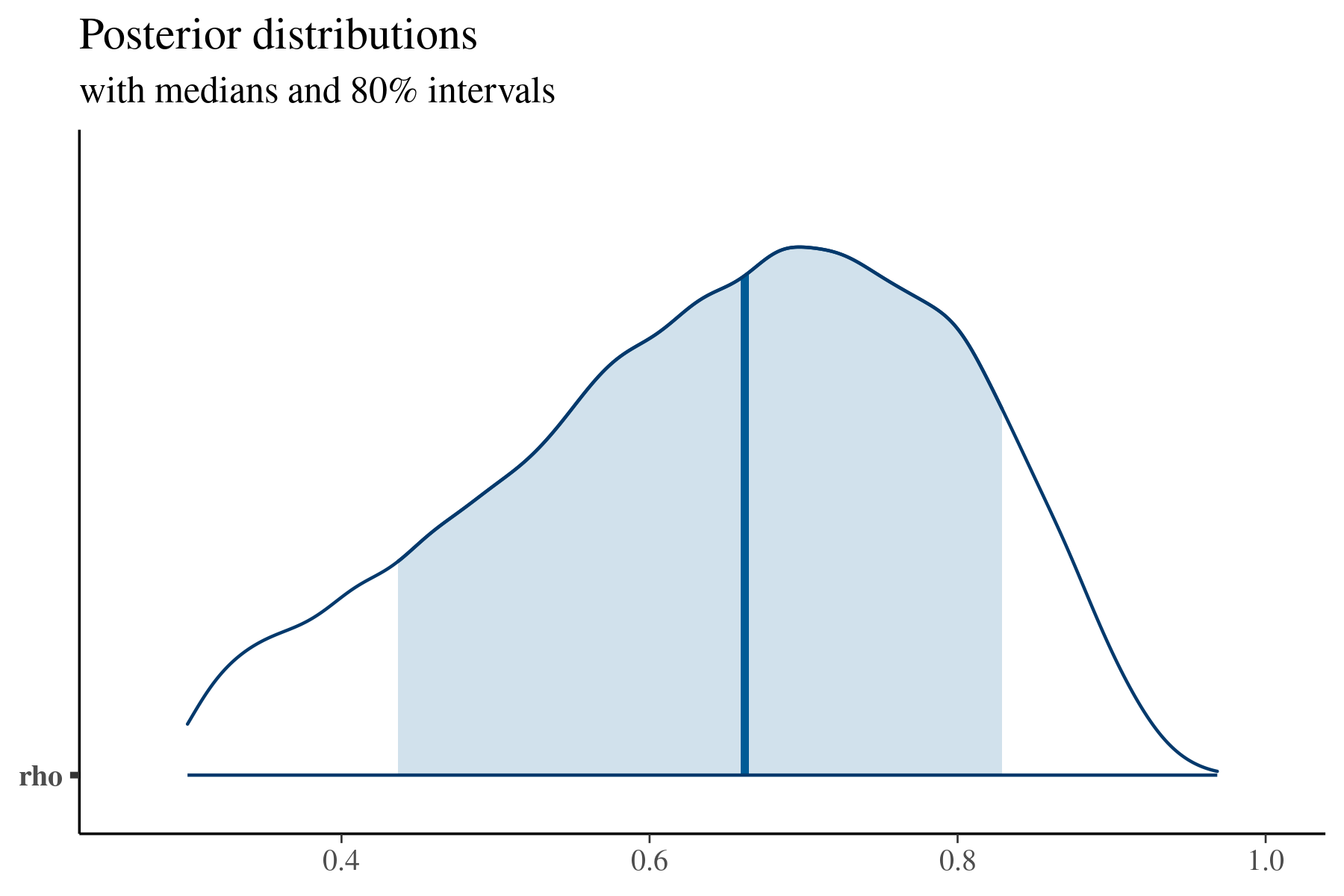
でした。BayesFactor関数の結果とは少し値が離れていますね…どこか間違えているのかもしれませんが、事後分布を見る限り問題は見受けられません。レプリカ交換法でも初期値は負の値にしていましたが、対数尤度$-∞$のエリアを越えて正の値にいけていたようです。
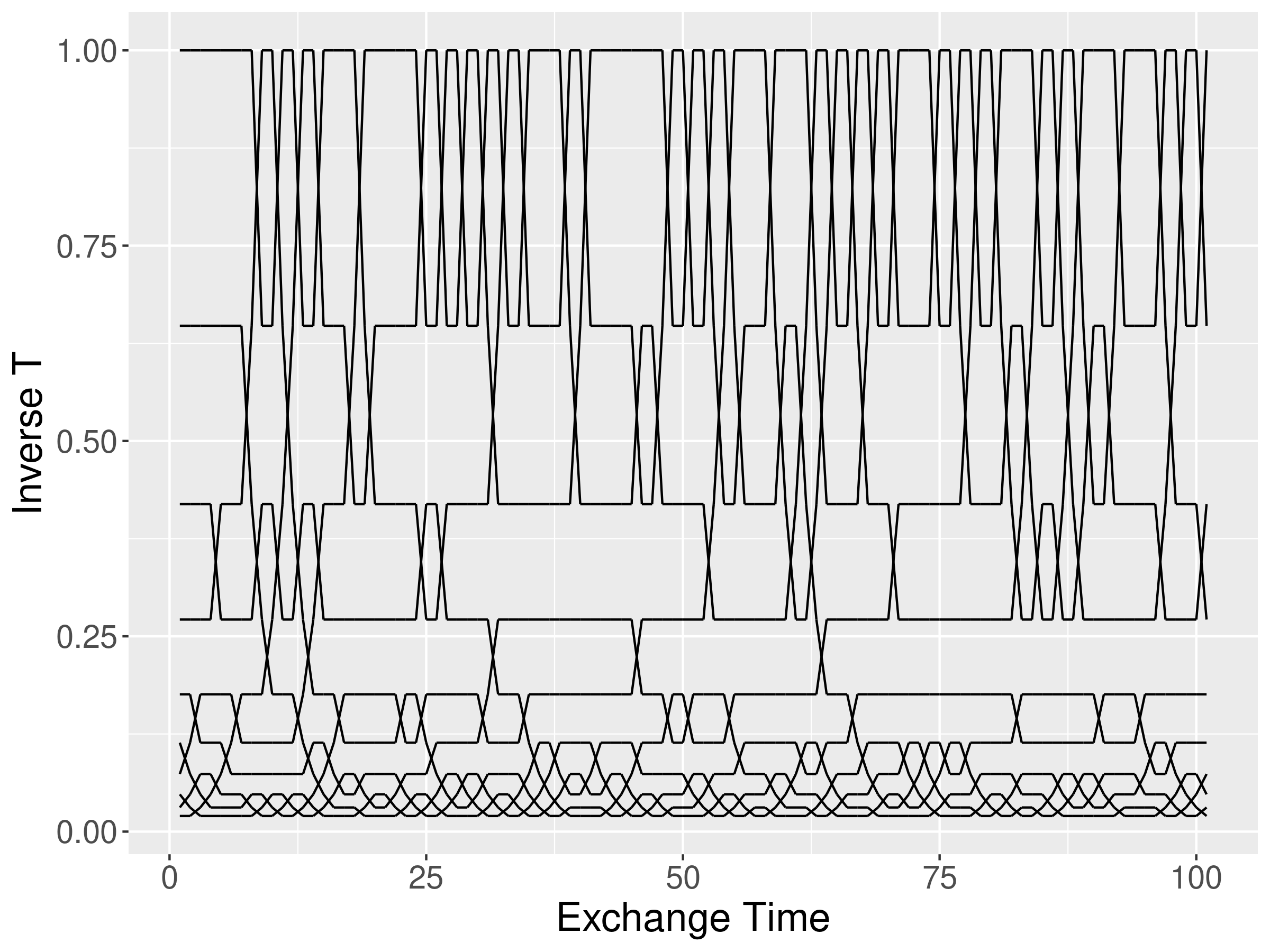
レプリカの交換状況を図化してみましたが、レプリカ同士の交換は問題なくできているようです。
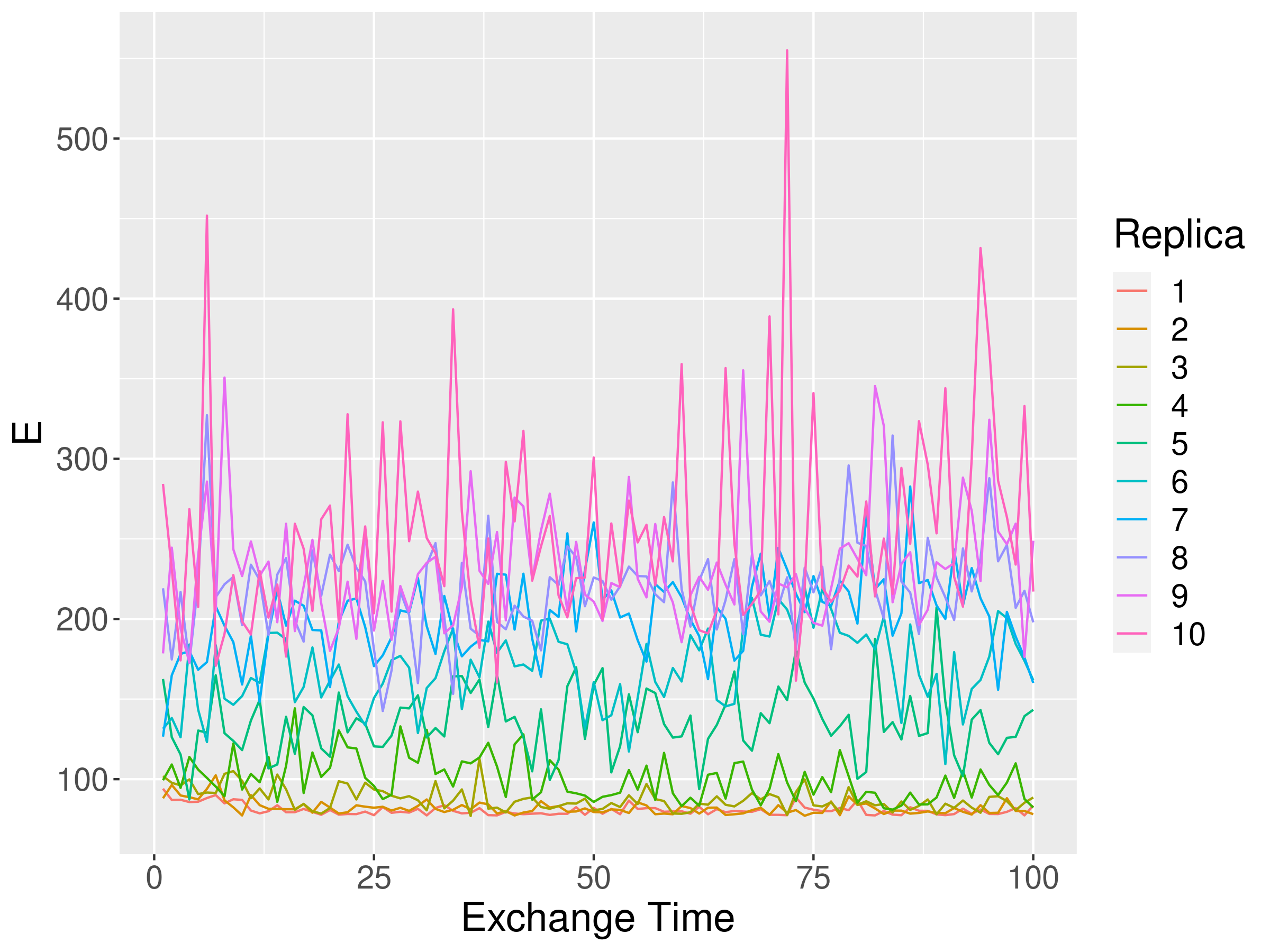
次にレプリカ交換タイムでのレプリカ毎のエネルギーを描画しましたが、レプリカ間の交換には支障なさそうなエネルギーであることが確認できます。
最後にトレースプロットの確認です。イテレーション50の段階で、$\rho$の値が負の値から脱却出来ていることが確認できました。
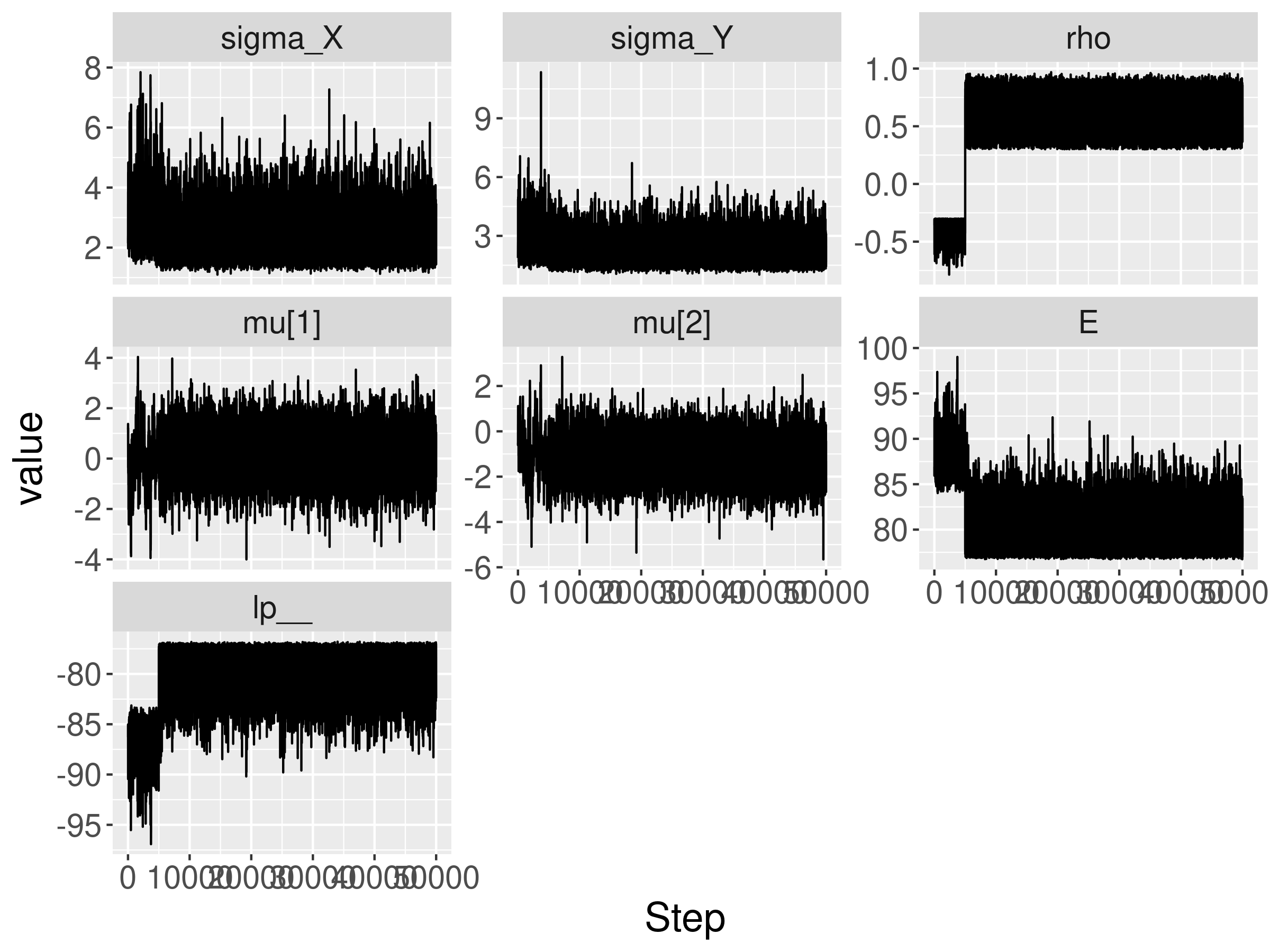
最終的に計算されたベイズファクターの値は解析解とは異なり、違和感がありましたが、レプリカ交換法自体はうまくいっていたようなので、よしとしましょう。
以上。
