ベイズファクターを使って相関の検定をやっていきます。
理論編はこちらを参照のこと。
サンプルデータの準備
本練習でつかうデータは、$\boldsymbol{\mu} = \left( 0, 0 \right)^T $、$\boldsymbol{\Sigma} = \left( \begin{array}{ccc} 4 & 3 \\ 3 & 4 \end{array} \right)$の二次元正規分布から10コ乱数を生成したものです。
よって$\rho = 0.75$ですね。
library(mvtnorm)
d <- rmvnorm(n=10, mean=c(0,0), sigma = matrix(c(4,3,3,4), ncol=2),method="chol")
2/sqrt(4)/sqrt(2)
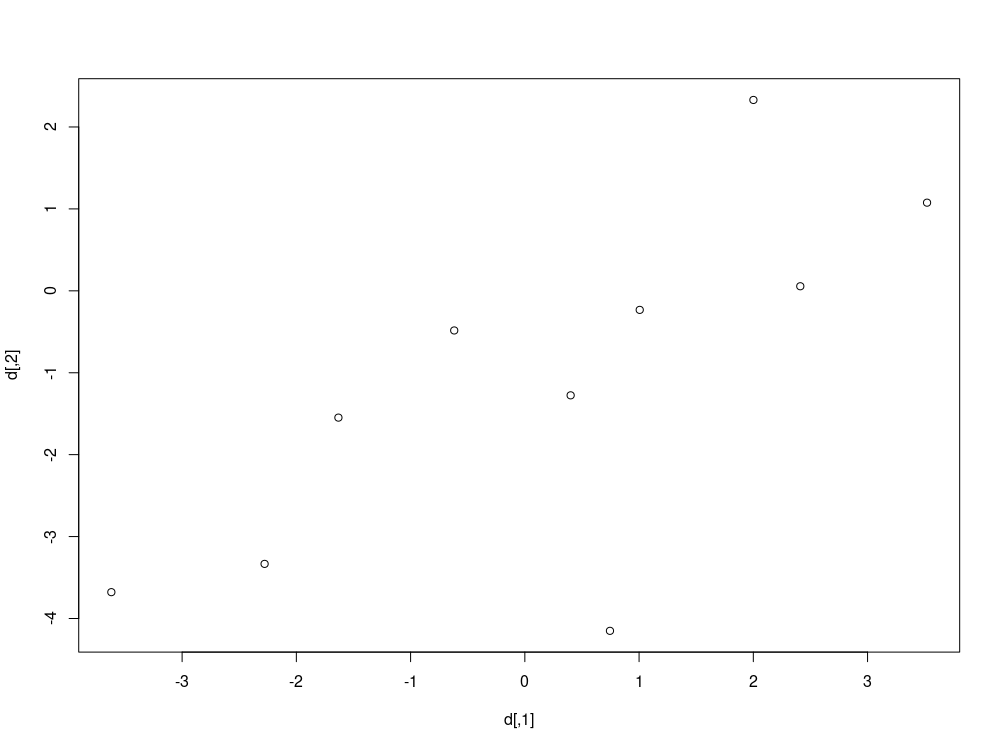
事前分布の設定
相関パラメータに対する理想的な事前分布の設定方法をおさらいします。
後で使うBayesFactorパッケージが推奨するデフォルトの設定は、$\kappa=3$です。
描画するとこんな感じです。
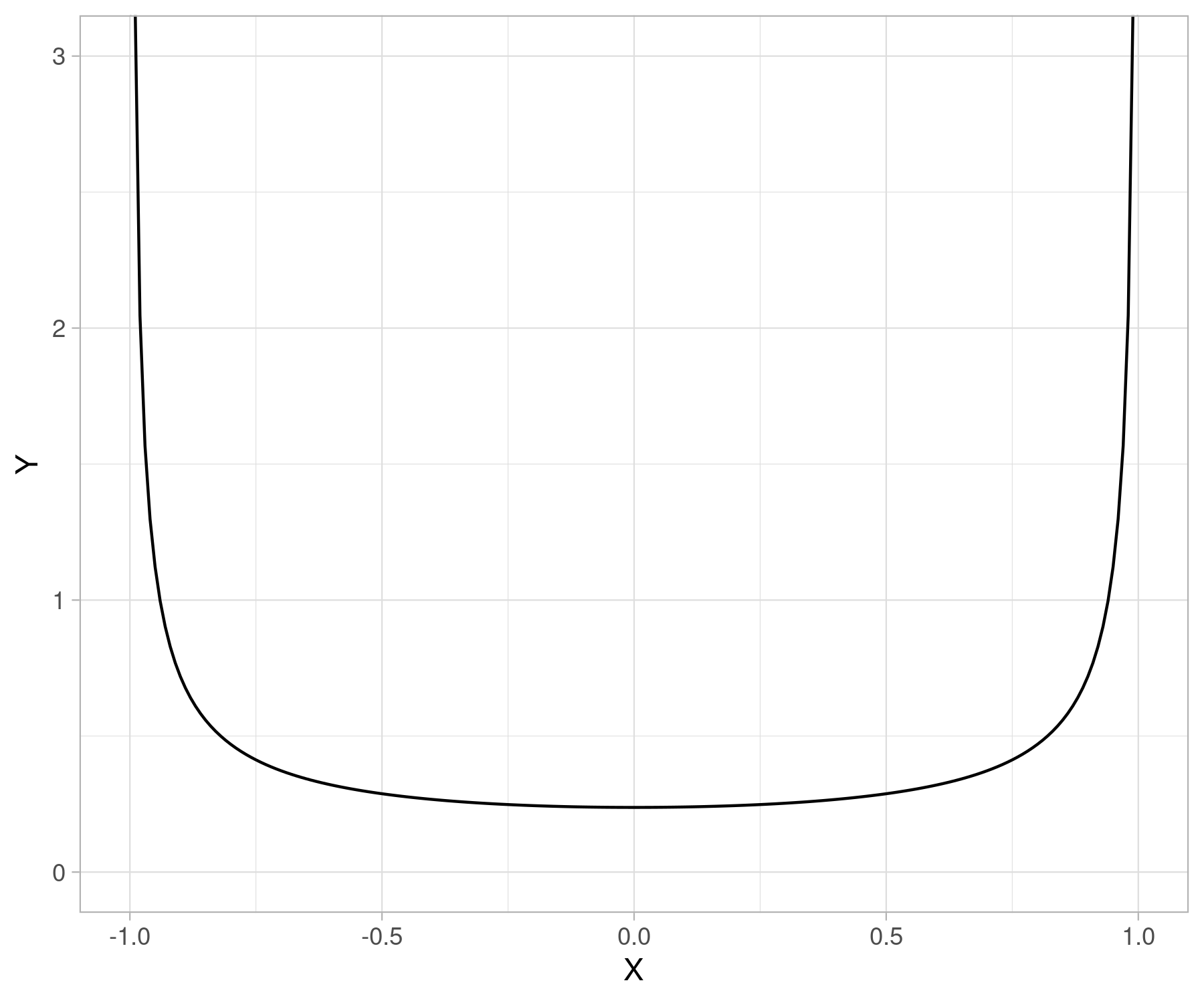
帰無仮説の設定
ここでは帰無仮説を複数設定して検定をしていきます。$H_{0_1}$は通常の統計学的検定で設定される帰無仮説と同じ設定です。相関がない場合を帰無仮説とします。
$$ H_{0_1}: \rho=0 $$
対立仮説は3つ用意します。
Hoijtink先生は、無制約仮説という、検定したいパラメータが定義される全領域を許容してやる仮説を設定することも推奨していますが、ここでは設定しません。詳細はこの本を参照のこと。
BayesFactor関数を使って計算
いつものごとく、誰でも簡単に解析的にベイズファクターを計算できることを目的に開発された、BayesFactorパッケージを使って計算してみます。
correlationBF(d[,1], d[,2], rscale = "medium")
# Bayes factor analysis
# --------------
# [1] Alt., r=0.333 : 3.549771 ±0%
#
# Against denominator:
# Null, rho = 0
# ---
# Bayes factor type: BFcorrelation, Jeffreys-beta*
correlationBF(d[,1], d[,2], rscale = "medium", nullInterval = c(-1,0))
# Bayes factor analysis
# --------------
# [1] Alt., r=0.333 -1<rho<0 : 0.2557948 ±NA%
# [2] Alt., r=0.333 !(-1<rho<0) : 6.809117 ±NA%
#
# Against denominator:
# Null, rho = 0
# ---
# Bayes factor type: BFcorrelation, Jeffreys-beta*
correlationBF(d[,1], d[,2], rscale = "medium", nullInterval = c(-0.3,0.3))
# Bayes factor analysis
# --------------
# [1] Alt., r=0.333 -0.3<rho<0.3 : 1.506277 ±NA%
# [2] Alt., r=0.333 !(-0.3<rho<0.3) : 5.814191 ±NA%
#
# Against denominator:
# Null, rho = 0
# ---
# Bayes factor type: BFcorrelation, Jeffreys-beta*
対立仮説$H_{1_1}$のときのベイズファクター（対立仮説が正しいエビデンス / 帰無仮説が正しいエビデンス）を$BF_{10_{1}}$と表現すると、それぞれのベイズファクターは下記の値となりました。
乱数生成したときの設定（$\rho = 0.75$）を考えるとそうおかしな結果ではなさそうです。
Bridgesamplingを使って計算
今度はブリッジサンプリングと呼ばれる手法を使ってベイズファクターを計算していきます。ここで使用するBridgesampling::bridge_sampler()関数は、ブリッジサンプリング方により、モデルの自由エネルギーや周辺尤度をMCMC結果から直接推定することができる便利な道具です。
bridge_sampler()を使う場合も、stanでモデルを組む必要があります。
まずは帰無仮説$H_{0_1}$を表現したstanコードです。
data {
int<lower=0> N; // sample size
vector[2] D[N]; // Data consists of X and Y
real Jeffreys_alpha;
real Jeffreys_beta;
//kappa : prior scale of rho
//Jeffreys_alpha : mean of prior(sigma^2) (sufficiently small values)
//Jeffreys_beta : variance of prior(sigma^2) (sufficiently small values)
}
parameters {
real<lower=0> sigma_X;
real<lower=0> sigma_Y;
vector[2] mu;
// mu consists of mu_X, mu_Y
// mu_X, mu_Y : mean of X and Y, respecttively
// sigma_X, sigma_Y : standard deviation of X and Y, respectively
// rho : correlation of X and Y
}
transformed parameters{
matrix[2,2] cov;
cov[1,1] = square(sigma_X);
cov[1,2] = 0;
cov[2,1] = 0;
cov[2,2] = square(sigma_Y);
}
model {
//model
for(n in 1:N){
target += multi_normal_lpdf(D[n] | mu, cov );
}
//prior
target += gamma_lpdf(square(sigma_X) | Jeffreys_alpha, Jeffreys_beta);
target += gamma_lpdf(square(sigma_Y) | Jeffreys_alpha, Jeffreys_beta);
target += normal_lpdf(mu | 0, 100);
}
$\rho$に不等式制約を課した仮説（以降、情報仮説と呼びます）を表現するStanコードは以下。
data{}ブロックでint model_typeというものを導入しています。これは、表現したい仮説に合わせて$0$または$1$を設定するもので、$0$を選択した場合、仮説によって相関パラメータの空間が分割されないモデル（例えば、$-0.3 < \rho < 0.3$）を表現します。逆に$1$を選択した場合、仮説によって相関パラメータの空間が2つに分割されてしまうモデル（例えば、$\rho < -0.3$、$\rho > 0.3$）を表現します。入力したint model_typeの値に対応して、function()ブロックで定義した事前分布のための関数stretched_symmetric_beta_lpdf()の機能がスイッチされることとなります。
functions{
real stretched_symmetric_beta_lpdf(real y, real kappa, real lower_rho, real upper_rho, int model_type){
if(model_type == 0)
if( y >= lower_rho && y <= upper_rho )
return
-log(inc_beta(1/kappa, 1/kappa, 0.5 * (upper_rho + 1)) - inc_beta(1/kappa, 1/kappa, 0.5 * (lower_rho + 1))) +
((kappa-2)/kappa) * log(2) - lbeta(1/kappa, 1/kappa) + ((1-kappa)/kappa) * log((1 - square(y)));
else
return negative_infinity();
if(model_type == 1)
if( y <= lower_rho || y >= upper_rho )
return
-log(1 - inc_beta(1/kappa, 1/kappa, 0.5 * (upper_rho + 1)) + inc_beta(1/kappa, 1/kappa, 0.5 * (lower_rho + 1))) +
((kappa-2)/kappa) * log(2) - lbeta(1/kappa, 1/kappa) + ((1-kappa)/kappa) * log((1 - square(y)));
else
return negative_infinity();
else
return negative_infinity();
}
}
data {
int<lower=0> N; // sample size
vector[2] D[N]; // Data consists of X and Y
real kappa;
real Jeffreys_alpha;
real Jeffreys_beta;
real<lower=-1, upper=1> lower_rho;
real<lower=-1, upper=1> upper_rho;
int model_type;
//kappa : prior scale of rho
//Jeffreys_alpha : mean of prior(sigma^2) (sufficiently small values)
//Jeffreys_beta : variance of prior(sigma^2) (sufficiently small values)
//model_type
}
parameters {
real<lower=0> sigma_X;
real<lower=0> sigma_Y;
real<lower=-1, upper=1> rho;
vector[2] mu;
// mu consists of mu_X, mu_Y
// mu_X, mu_Y : mean of X and Y, respecttively
// sigma_X, sigma_Y : standard deviation of X and Y, respectively
// rho : correlation of X and Y
}
transformed parameters{
matrix[2,2] cov;
cov[1,1] = square(sigma_X);
cov[1,2] = sigma_X * sigma_Y * rho;
cov[2,1] = sigma_X * sigma_Y * rho;
cov[2,2] = square(sigma_Y);
}
model {
//prior
target += stretched_symmetric_beta_lpdf(rho | kappa, lower_rho, upper_rho, model_type);
target += gamma_lpdf(square(sigma_X) | Jeffreys_alpha, Jeffreys_beta);
target += gamma_lpdf(square(sigma_Y) | Jeffreys_alpha, Jeffreys_beta);
target += normal_lpdf(mu | 0, 100);
//model
for(n in 1:N){
target += multi_normal_lpdf(D[n] | mu, cov);
}
}
これら2つのstanコードを使って、まずは帰無仮説$H_{0_1}$設定したときのベイズファクターを推定してみましょう。
$H_{1_1}$のときのベイズファクターを推定
分析の流れは、「帰無仮説（$H_{0_1}$）の場合の自由エネルギー推定」、「対立仮説の自由エネルギー推定」、「両者の自由エネルギーを比較」です。
今回、cmdstanを使っている環境上、bridge_sampler()の引数にはrstan::read_stan_csv()よりcmdstan結果から抽出したMCMCサンプルと、rstan::stan()でコンパイルしなおしたstanファイルを入れます。このひと手間がないと現状cmdstanでブリッジサンプリングしてくれません。
最後の計算では、
という変換をかませています。周辺尤度の対数$\log\left(p(x^n | M)\right)$はbridge_sampler()$logmlで抽出することができます。
# null model の自由エネルギーを推定 --------------------------------------------------
# Global variable : kappa, lower_rho, upper_rho, model_type, Jeffreys_alpha, Jeffreys_beta
kappa <- 3
Jeffreys_alpha <- 1e-5
Jeffreys_beta <- 1e-5
data_null <- list(D = d, N = nrow(d), Jeffreys_alpha=Jeffreys_alpha, Jeffreys_beta=Jeffreys_beta)
fit_null <- model_null$sample(
data = data_null,
parallel_chains = 4,
chains = 4,
iter_warmup = 1000,
iter_sampling = 10000,
refresh = 0,
save_warmup = TRUE
)
fit_cmdstan_null <- rstan::read_stan_csv(fit_null$output_files())
fit_rstan_null <- rstan::stan(paste0(getwd(),"/model/model_null.stan"),data=data_null,iter=0)
free_energy_null <- bridgesampling::bridge_sampler(fit_cmdstan_null,fit_rstan_null)$logml
# 対立仮説（-1 < rho < 1）の自由エネルギーを推定 ------------------------------------------------------------------
# Global variable : kappa, lower_rho, upper_rho, model_type, Jeffreys_alpha, Jeffreys_beta
kappa <- 3
Jeffreys_alpha <- 1e-5
Jeffreys_beta <- 1e-5
# Alternative
lower_rho <- -1
upper_rho <- 1
model_type <- 0
data_alt <- list(D = d, N = nrow(d), kappa=kappa,
Jeffreys_alpha=Jeffreys_alpha, Jeffreys_beta=Jeffreys_beta,
upper_rho=upper_rho, lower_rho=lower_rho, model_type=model_type)
fit_alt <- model_informative$sample(
data = data_alt,
parallel_chains = 4,
chains = 4,
iter_warmup = 1000,
iter_sampling = 10000,
refresh = 0,
save_warmup = TRUE
)
# caluculate the free energy of H_alternative
fit_cmdstan_alt <- rstan::read_stan_csv(fit_alt$output_files())
fit_rstan_alt <- rstan::stan(paste0(getwd(),"/model/model_informative.stan"),data=data_alt,iter=0)
free_energy_alt <- bridgesampling::bridge_sampler(fit_cmdstan_alt,stanfit_model = fit_rstan_alt)$logml
# 自由エネルギーを比較 --------------------------------------------------------------
exp(free_energy_alt - free_energy_null)
# [1] 3.118342
推定されたベイズファクターは、
$$ BF_{10_1} ≒ 3.12 $$
でした。BayesFactorパッケージの結果と少し違いますが、許容でしょうか。
$H_{0_2}$についても同様に推定してみましょう。
$H_{1_2}$のときのベイズファクターを推定
分析は先ほどとほぼ同じです。
# -1<p<0と0<p<1を比較 ---------------------------------------------------------
# Global variable : kappa, lower_rho, upper_rho, model_type, Jeffreys_alpha, Jeffreys_beta
kappa <- 3
Jeffreys_alpha <- 1e-5
Jeffreys_beta <- 1e-5
# Alternative
lower_rho <- 0
upper_rho <- 1
model_type <- 0
data_alt <- list(D = d, N = nrow(d), kappa=kappa,
Jeffreys_alpha=Jeffreys_alpha, Jeffreys_beta=Jeffreys_beta,
upper_rho=upper_rho, lower_rho=lower_rho, model_type=model_type)
fit_alt <- model_informative$sample(
data = data_alt,
parallel_chains = 4,
chains = 4,
iter_warmup = 1000,
iter_sampling = 10000,
refresh = 0,
save_warmup = TRUE
)
# caluculate the free energy of H_alternative
fit_cmdstan_alt <- rstan::read_stan_csv(fit_alt$output_files())
fit_rstan_alt <- rstan::stan(paste0(getwd(),"/model/model_informative.stan"),data=data_alt,iter=0)
free_energy_alt <- bridgesampling::bridge_sampler(fit_cmdstan_alt,stanfit_model = fit_rstan_alt)$logml
exp(free_energy_alt - free_energy_null)
# [1] 6.237172
推定されたベイズファクターは、
$$ BF_{10_2} ≒ 6.24 $$
でした。BayesFactorパッケージの結果と少し違いますが、これも許容でしょう。
$H_{1_3}$のときのベイズファクターを推定（失敗版）
最後に$H_{1_3}$のモデルの自由エネルギーを計算していこうと思うのですが、果たして$-0.3$から$0.3$の間に対数尤度マイナス無限大のエリアがあるモデルをうまくMCMCできるのでしょうか？
試しにMCMCの初期値をマイナスにした上で、走らせてみます。
# Global variable : kappa, lower_rho, upper_rho, model_type, Jeffreys_alpha, Jeffreys_beta
kappa <- 3
Jeffreys_alpha <- 1e-5
Jeffreys_beta <- 1e-5
# Informative2
lower_rho <- -0.3
upper_rho <- 0.3
model_type <- 1
init_list <- list(
list(rho = -0.5),
list(rho = -0.4),
list(rho = -0.6),
list(rho = -0.7)
)
data_informative <- list(D = d, N = nrow(d), Jeffreys_alpha=Jeffreys_alpha, Jeffreys_beta=Jeffreys_beta,
upper_rho = upper_rho, lower_rho= lower_rho, kappa=kappa, model_type=model_type)
fit_informative <- model_informative$sample(
data = data_informative,
parallel_chains = 4,
chains = 4,
iter_warmup = 1000,
iter_sampling = 10000,
refresh = 0,
save_warmup = TRUE,
adapt_delta = 0.9,
init = init_list
)
さらにMCMCサンプルを描画してみると…
fit_cmdstan_informative <- rstan::read_stan_csv(fit_informative$output_files())
posterior <- as.matrix(fit_cmdstan_informative)
plot_title <- ggtitle("Posterior distributions",
"with medians and 80% intervals")
mcmc_areas(posterior,
pars = c("rho"),
prob = 0.8) + plot_title
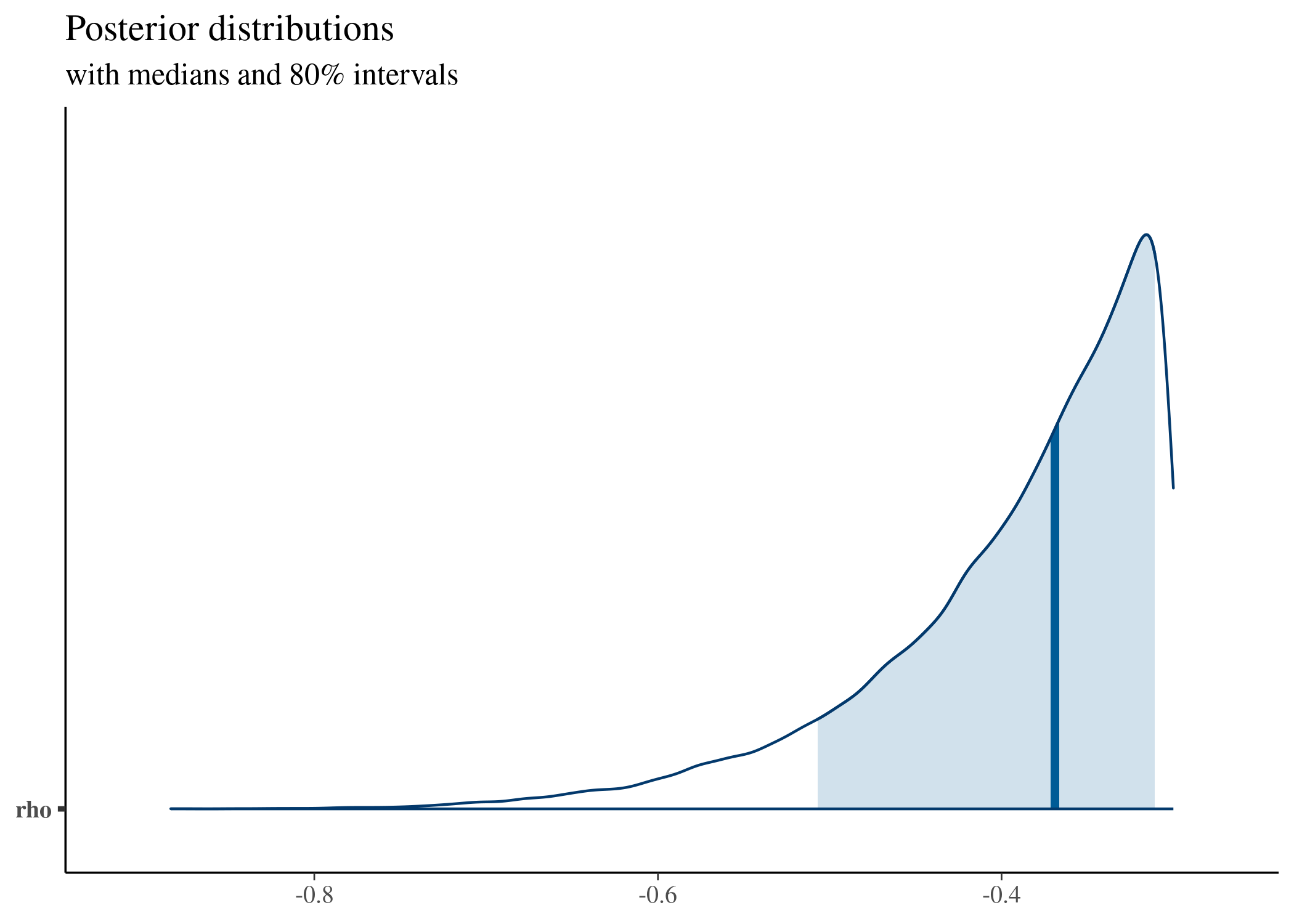
サンプルデータの値より、正しく収束した場合の$\rho$のMCMCサンプルは正の値、特に0.75あたりをうろうろするはずなのですが、今回のMCMCは対数尤度$-∞$の壁を超えられず、そうは行っていないことがわかります。
これを解決するためには、レプリカ交換MCMC法と呼ばれるアルゴリズムを実行してやる必要があるのですが、それについては次の記事で紹介したいと思います。
