はじめに

少しご無沙汰してしまい、また読者様から重くないやつを定期的にと助言いただきましたので、少し短めの投稿を記事作成のリハビリもかねてしてみようと思います

今回はそもそもこのブログで扱っているモデリングとは何だったのか？について改めて書いてみようと思います。さらに今後の記事では続きとしてモデル選択の基準、特にベイズで利用できるWAIC（広く使える情報量基準）について書いてみようと思っています。ただし、難しいことまではよくわからないので、感覚で理解できているところまで。

モデリング

モデリングとは

そもそもの話です。

統計解析ではデータが生成されるメカニズムを組み立てることでデータの解釈を進めていきます。このような活動をモデリングと呼んでいます。ただし、あるデータに対する数理モデルの候補は通常一つではありません。

例として、今回は回帰分析等のサンプルデータとしてよく用いられるアヤメデータを用います。アヤメデータにはいくつかの変数がありますが、GGally::ggpairs()で一気に視覚化・相関係数を算出してみます。これぞ業務効率化。

library(GGally)
p <- GGally::ggpairs(iris, aes(colour=Species))
p

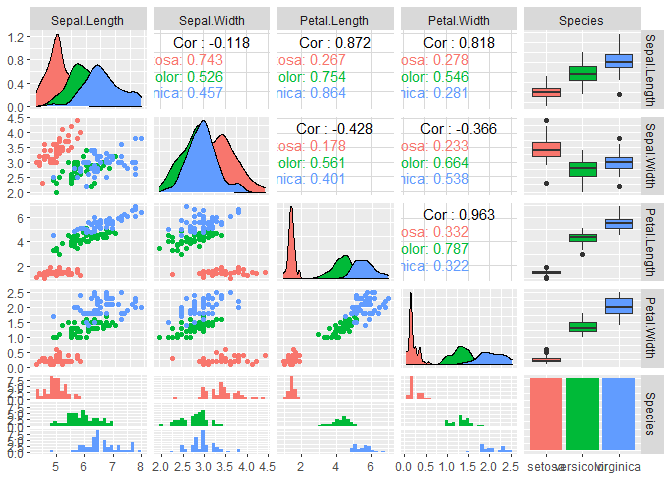
結果を見ると、花びらの長さ（Peral.Length）と幅（Petal.Width）には強い正の相関（0.963）があることが分かります。他にも様々な関係性が確認できますが、以降では花びらの長さを説明するためのモデルを構築していきます。

モデル1

はじめは最も単純なモデルから。まずは花びらの幅のみで花びらの長さを説明する式です。

$\begin{matrix} (1) & μ_{n} = α x_{n} + β \end{matrix}$ $\begin{matrix} (2) & y_{n} \sim N o r m a l (μ_{n}, σ) \end{matrix}$ $n = 1, 2, \dots, N$

ここで、 $N$ はデータの数、 $Y = (y_{1}, y_{2}, \dots, y_{N})$ は花びらの長さ、 $X = (x_{1}, x_{2}, \dots, x_{N})$ は花びらの幅とします。

上の式の意味を見てみましょう。

まず、これまで全く説明していませんでしたが、 $(2)$ 式で使用した数学記号「 $\sim$ 」は「確率変数（左辺）が確率分布（右辺）に従う」という意味です。
また $N o r m a l ()$ は正規分布（ガウス分布）を意味します。確率変数の記号の後ろにつく「 $()$ 」には各確率分布のパラメータを明記するのが常です。

正規分布の確率密度関数 $f (x)$ は以下となり、パラメータは平均 $μ$ 、標準偏差 $σ$ となります。

$f (x) = \frac{1}{\sqrt{2 π} σ} e x p [\frac{- {(x - μ)}^{2}}{s σ^{2}}]$

よって、 $(2)$ 式は確率変数 $Y_{n}$ が平均 $μ_{n}$ 、標準偏差 $σ$ の正規分布に従うことを意味します。
さらに $(1)$ 式では $μ_{n}$ が $α x_{n} + β$ という $x$ を用いた線形予測子によって計算されるとしています。

ちなみに先に挙げた式を用いて平均0、標準偏差1の正規分布の確率密度関数を視覚化すると、以下のようになります。

library(ggplot2)
x <- seq(-5,5,0.1)
y <- (1/sqrt(2*pi))*exp(-x^2/2)
p <- ggplot(data=data.frame(X=x,Y=y)) + theme_light()+
  geom_line(aes(x=X,y=Y)) + xlab(NULL) + ylab(NULL)
p

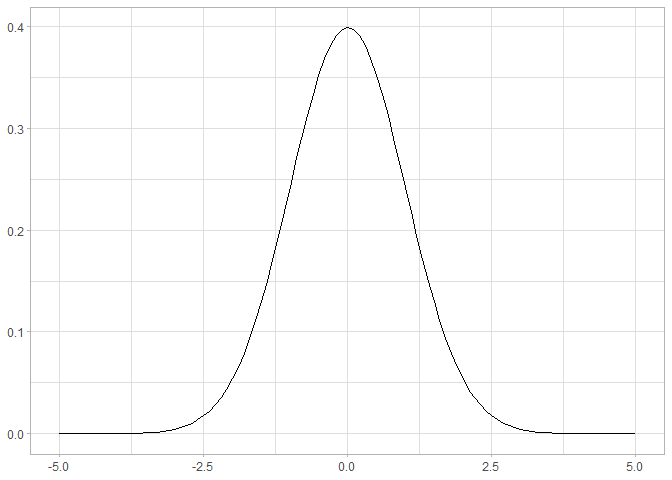
このように、正規分布は左右対称であり、平均と標準偏差自体がパラメータとなる使いやすい分布であるため、様々な統計解析に活用されます。最もよく用いられるのは、今回の例のように連続型変数の誤差の分布を仮定するときではないだろうか？

glm()を用いてこのモデルのパラメータを推測した結果が以下になります。

library(ggeffects)
res <- glm(data=iris, formula = Petal.Length ~ Petal.Width, family=gaussian)

summary(res)

##
## Call:
## glm(formula = Petal.Length ~ Petal.Width, family = gaussian,
##     data = iris)
##
## Deviance Residuals:
##      Min        1Q    Median        3Q       Max  
## -1.33542  -0.30347  -0.02955   0.25776   1.39453  
##
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  1.08356    0.07297   14.85   <2e-16 ***
## Petal.Width  2.22994    0.05140   43.39   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for gaussian family taken to be 0.2286808)
##
##     Null deviance: 464.325  on 149  degrees of freedom
## Residual deviance:  33.845  on 148  degrees of freedom
## AIC: 208.35
##
## Number of Fisher Scoring iterations: 2

res_p <- ggeffects::ggpredict(res, terms="Petal.Width")
ggplot() + theme_light(base_size=11) +
  geom_point(data=iris, aes(x=Petal.Width, y=Petal.Length), shape=1) +
  geom_line(data=res_p, aes(x=x, y=predicted)) +
  geom_ribbon(data=res_p, aes(x=x, ymin=conf.low, ymax=conf.high), alpha=0.1)

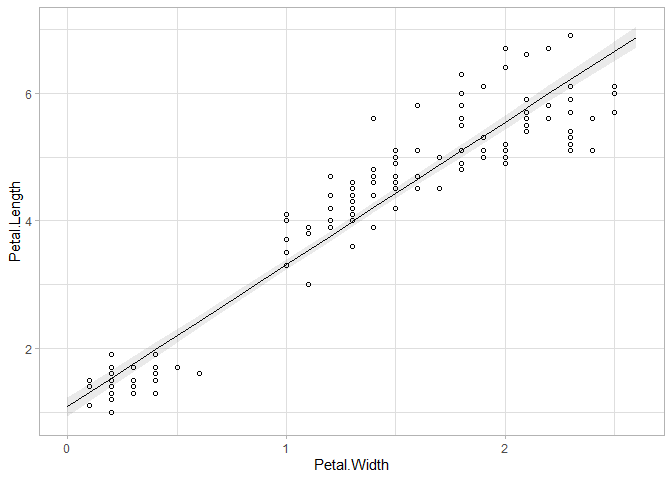
結果がいろいろと書いてありますが、今回はCoefficientsのところから、構築したモデルに対する以下の結果を確認するのみとします(Devianceなどについて復習するのが面倒になった顔)。信頼区間の算出方法も実はよくわかっていません…。ベイズ的なアプローチならこのあたりの理論を事後分布で回避できるのに…

$μ_{n} = 1.08356 X_{n} + 2.22994$

ここまで読んで、エクセルのグラフ機能についている近似曲線（線形近似）と何が違うのか、と思ったかもしれません。実は以上の分析はエクセルでもは全く同じ結果が得られるはずです。違うのは解析手法（最小二乗法か最尤法）くらいかもしれません。しかし単に線形補完をしているのだ、という認識ではなく、上のように統計的なモデルが背景にあるということを理解していると、データに対してより適切な仮定を置くことが可能になります。

はっきり言いますが、ガウス分布を仮定した線形回帰の場合、①目的変数はすべての実数を定義域に持つ連続変数、②目的変数の誤差が正規分布に従うと仮定するため、これらの条件を満たしたデータでないとガウス分布を仮定した線形回帰の結果を信頼することはできない。ということ！
上記の仮定を無視した例としては、離散型変数を目的変数に置いたり、ガウス分布を仮定した線形回帰をあてはめた際の誤差の分布をQQプロットや正規性の検定等で確認しない場合が挙げられます。

モデル2

モデル1は単回帰と呼ばれ、一つの説明変数しか設定しない分析でしたが、説明変数は一つである必要はありません。より多くの情報を持たせた方がモデルの精度が向上することも十分あります。複数の説明変数が存在する場合、重回帰と呼ばれます。

GGally::ggpairs()の結果からアヤメの種類（Species）も花びらの長さに影響しそうだと判断し、説明変数に先ほどの花びらの長さに加えてアヤメの種類（Species）を追加してみます。モデル式は以下になります。

$μ_{n} = α x_{n} + β_{1} V e r s i c o l o r + β_{2} V i r g i n i a + γ$ $y_{n} \sim N o r m a l (μ_{n}, σ)$ $n = 1, 2, \dots, N$

説明変数に $V e r s i c o l o r$ と $V i r g i n i a$ を追加しました。これらはアヤメの種類を指しますが、 $n = 1, 2, 3 \dots$ としたときに種類がそれぞれに該当したときのみ1をとり、そうでない場合は0をとります。カテゴリカルな説明変数はダミー変数と呼ばれ、通常このような対応をとります。

res <- glm(data=iris, formula = Petal.Length ~ Petal.Width + Species, family=gaussian)

summary(res)

##
## Call:
## glm(formula = Petal.Length ~ Petal.Width + Species, family = gaussian,
##     data = iris)
##
## Deviance Residuals:
##      Min        1Q    Median        3Q       Max  
## -1.02977  -0.22241  -0.01514   0.18180   1.17449  
##
## Coefficients:
##                   Estimate Std. Error t value Pr(>|t|)    
## (Intercept)        1.21140    0.06524  18.568  < 2e-16 ***
## Petal.Width        1.01871    0.15224   6.691 4.41e-10 ***
## Speciesversicolor  1.69779    0.18095   9.383  < 2e-16 ***
## Speciesvirginica   2.27669    0.28132   8.093 2.08e-13 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for gaussian family taken to be 0.1426948)
##
##     Null deviance: 464.325  on 149  degrees of freedom
## Residual deviance:  20.833  on 146  degrees of freedom
## AIC: 139.57
##
## Number of Fisher Scoring iterations: 2

res_p <- ggeffects::ggpredict(res, terms=c("Petal.Width[all]","Species"), rawdata=T)

library(RColorBrewer)
col=brewer.pal(3,"Set1")

ggplot() + theme_light(base_size=11) +
  geom_point(data=iris, aes(x=Petal.Width, y=Petal.Length, colour=Species), shape=1) +
  geom_line(data=res_p, aes(x=x, y=predicted, colour=group)) +
  geom_ribbon(data=res_p, aes(x=x, ymin=conf.low, ymax=conf.high, fill=group), alpha=0.3) +
    scale_fill_manual(values=col) + scale_color_manual(values=col)

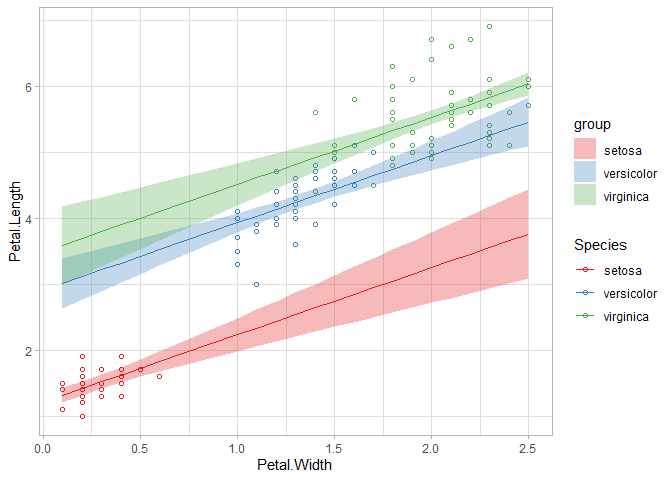
推定結果は以下の通りです。

$μ_{n} = 1.01871 X_{n} + 1.69779 V e r s i c o l o r + 2.27669 V i r g i n i c a + 1.21140$

このように、モデリングではある変数を説明するための変数を追加したり取り除いたりし、結果を確認しながら最終的にどの変数を用いるか検討していきます。

モデル3

モデル1およびモデル2は、目的変数の誤差に正規分布を仮定したもので、一般線形モデルとも呼ばれるモデルでした。しかし目的変数の性質によっては誤差が正規分布でかていできない場合もあります。その場合に有効なのが一般化線形モデル（GLM）です。GLMでは誤差に正規分布だけでなく二項分布やポアソン分布、負の二項分布など様々な分布を一般化して扱います。

今回の例の場合、花びらの長さは負の値をとらないことから厳密には正規分布を仮定できません。そこで非負の値を定義域に持つ連続変数に適用できるガンマ分布を誤差が従う分布に仮定します。

モデル式は以下になります。ガンマ分布はshapeパラメータ $k$ とrateパラメータ $λ$ をもち、 $k$ は常に一定、 $λ$ は線形予測子の変化に応じて変化すると仮定します。また目的変数の期待値が非負の値をとることを考慮し、リンク関数として $l o g$ をを設定しています。線形予測子と目的変数の期待値を関連させるのがここでのリンク関数の役割です。下の $(4)$ 式を変形すると $l o g (E (y_{n})) = μ_{n}$ となり、 $e x p$ の逆関数である $l o g$ が目的変数の期待値を線形予測子と関連させていることになります。こうすることで $(2)$ 式の目的変数の期待値が非負の値をとることがないという特性を満足させることが出来ます。

$\begin{matrix} (3) & μ_{n} = α x_{n} + β_{1} V e r s i c o l o r + β_{2} V i r g i n i a + γ \end{matrix}$

$\begin{matrix} (4) & E (y_{n}) = k / λ_{n} = e x p (μ_{n}) \end{matrix}$

$\begin{matrix} (5) & y_{n} \sim G a m m a (k, λ_{n}) \end{matrix}$ $n = 1, 2, \dots, N$

res <- glm(data=iris, formula = Petal.Length ~ Petal.Width + Species, family=Gamma(link="log"))

summary(res)

##
## Call:
## glm(formula = Petal.Length ~ Petal.Width + Species, family = Gamma(link = "log"),
##     data = iris)
##
## Deviance Residuals:
##      Min        1Q    Median        3Q       Max  
## -0.34682  -0.05608  -0.00637   0.05856   0.28685  
##
## Coefficients:
##                   Estimate Std. Error t value Pr(>|t|)    
## (Intercept)        0.31996    0.01716  18.643  < 2e-16 ***
## Petal.Width        0.24062    0.04005   6.008 1.43e-08 ***
## Speciesversicolor  0.80728    0.04760  16.960  < 2e-16 ***
## Speciesvirginica   0.90676    0.07400  12.253  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for Gamma family taken to be 0.009874458)
##
##     Null deviance: 44.6546  on 149  degrees of freedom
## Residual deviance:  1.4566  on 146  degrees of freedom
## AIC: 93.256
##
## Number of Fisher Scoring iterations: 4

res_p <- ggeffects::ggpredict(res, terms=c("Petal.Width[all]","Species"), rawdata=T)

library(RColorBrewer)
col=brewer.pal(3,"Set1")

ggplot() + theme_light(base_size=11) +
  geom_point(data=iris, aes(x=Petal.Width, y=Petal.Length, colour=Species), shape=1) +
  geom_line(data=res_p, aes(x=x, y=predicted, colour=group)) +
  geom_ribbon(data=res_p, aes(x=x, ymin=conf.low, ymax=conf.high, fill=group), alpha=0.3) +
    scale_fill_manual(values=col) + scale_color_manual(values=col)

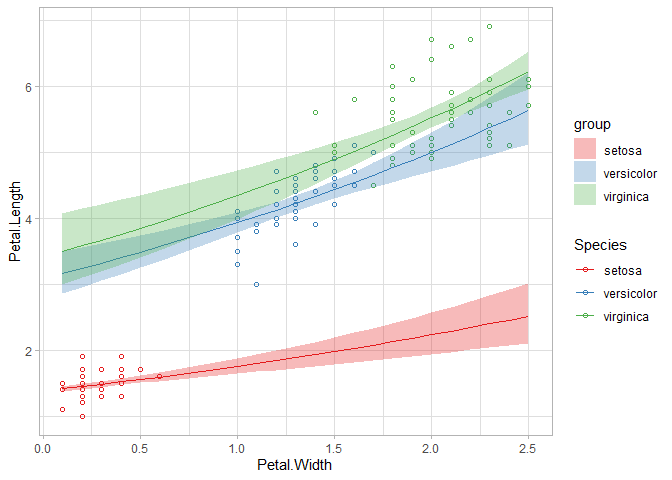
推定結果は以下の通りです。

$μ_{n} = 0.24062 x_{n} + 0.80728 V e r s i c o l o r + 0.90672 V i r g i n i a + 0.31996$

結果の解釈はお任せしますが、モデルの背景にある仮定をデータの特徴に合わせてより適切なものに修正した形になります。

まとめ

今回はモデリングとは？ということで記事を書いてみました。まとめると以下のような作業がデータの生成過程を組み立てる一連の活動を構成するのかな、と思います。

変数の取捨選択
確率変数やその誤差が従う分布を仮定

次はモデルの取捨選択を手助けする情報量基準についてまとめてみようかなとおもっています。

2020.10.03 00:00

モデリングと情報量基準その１～モデリングとは？～