はじめに

回帰に関する記事です。本記事では以前の記事で扱った多項ロジスティック回帰をrstanで実行します。

本記事の構成は以下の通りとします。

はじめに
モデルの確認
データの入手・整形
Stanによる多項ロジスティック回帰の実装
結果の確認
結果の描画
まとめ

モデルの確認

以前の記事でも紹介した多項ロジスティック回帰モデルの一般式を再掲します。
従属変数 $Y$ 、説明変数 $X$ について、 $Y = (y_{1}, \dots, y_{n}, \dots, y_{N})^{T}$ 、 $X = (x_{1}, \dots, x_{n}, \dots, x_{N})^{T}$ とし、さらに $x_{n} = (x_{1 n}, \dots, x_{d n}, \dots, x_{D n})$ としたとき、多項ロジスティック回帰のモデル式は以下になります。 $N$ はサンプルサイズ、 $D$ は説明変数の次元です。

$μ_{n} = \vec{a} + \vec{b_{1}} x_{n 1} + \dots + \vec{b_{d}} x_{n d} + \dots + \vec{b_{D}} x_{n D}$ $θ_{n} = s o f t m a x (μ_{n})$ $y_{n} \sim C a t e g o r i c a l (θ_{n})$ $(n = 1, \dots, N)$

ここで $μ = (μ_{1}, \dots, μ_{n}, \dots, μ_{N})$ $θ = (θ_{1}, \dots, θ_{n}, \dots, θ_{N})$

$μ_{n}, θ_{n}, \vec{a}, \vec{b_{1}}, \dots, \vec{b_{D}}$ は長さ $K$ のベクトルです。

データの入手・整形

以前の記事でも扱ったデータを用います。今回もprog(200人の生徒がgeneral、vocation、academicの3つの授業から選んだ授業)を従属変数とし、ses(家庭の経済状況)、write(書く力)を従属変数とします。

以下の通りStanに指定するデータに整形していきます。

library(makedummies)
library(tidyr)
library(dplyr)
library(foreign)

ml <- read.dta("https://stats.idre.ucla.edu/stat/data/hsbdemo.dta")

## progの3引数を数字に置き換えるための表を作成
progid <- c(1,2,3)
names(progid) <- c("academic","general","vocation")

## makedummies()はsesに対してダミー変数を作成するために使用
## interceptは切片項
d <- ml %>% cbind(makedummies::makedummies(ml,basal_level = F, col = "ses")) %>%
  mutate(progid = progid[paste(prog)]) %>% select(c(ses_middle, ses_high, write, progid)) %>%
  cbind(intercept=rep(1,nrow(ml)))

head(d,10)

##    ses_middle ses_high write progid intercept
## 1           0        0    35      3         1
## 2           1        0    33      2         1
## 3           0        1    39      3         1
## 4           0        0    37      3         1
## 5           1        0    31      3         1
## 6           0        1    36      2         1
## 7           1        0    36      3         1
## 8           1        0    31      3         1
## 9           1        0    41      3         1
## 10          1        0    37      3         1

ここで、本データ用に設定したモデル式における係数の呼称を以下の通り定義しておきます。

$\frac{P (p r o g = g e n e r a l)}{P (p r o g = a c a d e m i c)} = \exp (b_{11} + b_{21} (s e s = m i d d l e) + b_{31} (s e s = h i g h) + b_{41} w r i t e)$

$\frac{P (p r o g = v o c a t i o n)}{P (p r o g = a c a d e m i c)} = \exp (b_{12} + b_{22} (s e s = m i d d l e) + b_{32} (s e s = h i g h) + b_{42} w r i t e)$

Stanによる多項ロジスティック回帰の実装

多項ロジスティック回帰を実行するStanコードは以下のようになります。

//(model1.stan)
//dataブロック：データを指定
data{
  int<lower=2> K; //カテゴリ数
  int<lower=1> N; //サンプルサイズ
  int<lower=1> D; //データ項目数+切片項の数（１）
  int<lower=1, upper=K> y[N]; //prog
  matrix[N,D] x; //説明変数と切片項
  int N_new; //予測点の数
  matrix[N_new,D] x_new; //予測点群
}

//transformed dataブロック：新しくデータを生成 ここではmuの区別化の為の0ベクトルを生成
transformed data{
  vector[D] Zeros;
  Zeros = rep_vector(0, D);
}

//parameterブロック：パラメータを定義
parameters{
  matrix[D, K-1] b;
}

//transformed parameterブロック：parameterブロックで指定したパラメータを変形 ここでは0ベクトルと結合
transformed parameters{
  matrix[D,K] beta;
  beta = append_col(Zeros, b);
}

//modelブロック：モデルを定義
model{
  matrix[N,K] mu;
  mu = x * beta;
  for(n in 1:N){
    y[n] ~ categorical_logit(mu[n]);
  }
}

//generated quantitiesブロック：生成量を定義 ここでは確率に関する予測値mu_newとオッズ比の変量exp(b)を生成
generated quantities{
  matrix[D, K-1] ratio;//オッズ比の変量
  vector[K] pred[N_new];//予測点において各programが選ばれる確率
  matrix[N_new, K] mu_new;
  mu_new = x_new * beta;
  for(n in 1:N_new){
    pred[n,] = softmax(mu_new[n,]);
  }
  ratio = exp(b);
}

parameterブロックで指定した係数 $b$ の行番号・列番号の組み合わせが、先ほど定義したモデル式における係数の修飾番号に一致します。例えば、 $b [1, 2]$ はモデル式における $b_{12}$ に対応します。

Categorical_logit()はStanに実装された便利な関数で、Stan内部でsoftmaxを実行してくれます。つまり、y[n] ~ categorical_logit(mu[n]')とy[n] ~ Categorical(softmax(mu[n]'))はともに以下に示す処理を実行してくれます。

$y [n] \sim C a t e g o r i c a l (s o f t m a x (m u [n]))$

(注：上に示した実装ではコード表現の都合上categorical_logit()とsoftmax()の引数をそれぞれmu[n]、mu_new[n,]としていますが、softmax()は列ベクトルにしか対応していないので、実装では必ずベクトルや行列を転置させる命令である'を引数の後ろにつけてください！)

この部分についてもう少し補足すると、 $P (y [n] = 1) = s o f t m a x (m u [n,]) [1]$ $P (y [n] = 2) = s o f t m a x (m u [n, 2]) [2]$ $P (y [n] = 3) = s o f t m a x (m u [n, 3]) [3]$ という関係になっています。ここでは $b e t a [, 1] = 0$ とすることで $m u [, 1] = 0$ とし、またデータの整形において $a c a d e m i c \to 1, g e n e r a l \to 2, v o c a t i o n \to 3$ としているので、以下の通り $P (y [n] = 1 (a c a d e m i c))$ について固定・基準化していることになります。

$P (y [n] = 1 (a c a d e m i c)) = \frac{1}{\sum_{k = 1}^{K} \exp (m u [n, k])}$

また、上記の実装ではパラメータのbに事前分布を指定していませんが、Stanでは事前分布を指定しない場合、十分に幅の広い一様分布が自動で設定されます。そのため、パラメータに関する事前の設定要件が無い場合は、事前分布に何も指定しなくても無情報事前分布が設定されるため問題ありません。

model1に基づいてサンプリングを命令するコードは以下のようになります。

#(run_model1)
library(rstan)
x <- d[,c(5,1,2,3)]
y <- d[,"progid"]
K <- 3
N <- nrow(x)
D <- ncol(x)
x_new <- data.frame(rep(1,123),c(rep(0,41),rep(1,41),rep(0,41)),c(rep(0,82),rep(1,41)), write = rep(c(30:70),3))
N_new <- nrow(x_new)

fit0 <- stan(file = "model1.stan", data = list(x=x,y=y,K=K,N=N,D=D,x_new=x_new,N_new=N_new), seed=123, war=500, iter=1500, chains = 4)

rstan::stan()の引数について説明しておきます。

file：stanファイルを指定
data：必要なデータをリスト型で指定
war： warm up期間を指定
iter：waru up期間を含んだchainの長さ(iteration)を指定
chain：chain数を指定
seed：乱数の種類を指定

$x_{n e w}$ はパラメータのMCMCサンプルにもとづいて $P (y [n_{n e w}] = 1), P (y [n_{n e w}] = 2), P (y [n_{n e w}] = 3), n_{n e w} = 1, \dots, N_{n e w}$ の予測値を算出する際に、説明変数 $x$ がとる組み合わせを指定したものです。予測値は、MCMCでは生成量のサンプリングとして扱うため、generated quantitiesブロックで指定することになります。

結果の確認

MCMCの収束の確認

MCMCの実行後、まずはちゃんと収束していることを確認する必要があります。以下ではモデルの係数についてtracsplotを描画し、収束の確認を行います。

library(ggmcmc)
library(bayesplot)
posterior_fit0_1 <- rstan::extract(fit0, inc_warmup=TRUE, permuted=FALSE)
color_scheme_set("mix-blue-pink")
p <- mcmc_trace(posterior_fit0_1, regex_pars = c("b"), n_warmup = 500,
                facet_args = list(ncol = 2))+ theme_bw(base_size=12) + theme(legend.position = "bottom")
p

どの係数も早い段階で一つの値に収束しているようです。ここではwarm upを500に設定していますが、十分すぎるwarm up であることが確認できます。

MCMCの収束を確認する方法はtracsplotを用いた視覚的な判断だけでなく、数値基準も用意されています。

options(max.print = 80)
fit0

## Inference for Stan model: model1.
## 4 chains, each with iter=1500; warmup=500; thin=1;
## post-warmup draws per chain=1000, total post-warmup draws=4000.
##
##                  mean se_mean     sd    2.5%     25%     50%     75%   97.5%
## b[1,1]           2.89    0.03   1.16    0.62    2.11    2.90    3.66    5.12
## b[1,2]           5.36    0.03   1.13    3.17    4.61    5.32    6.14    7.57
## b[2,1]          -0.54    0.01   0.45   -1.41   -0.83   -0.53   -0.24    0.33
## b[2,2]           0.32    0.01   0.48   -0.64    0.00    0.31    0.64    1.28
## b[3,1]          -1.19    0.01   0.52   -2.27   -1.53   -1.19   -0.84   -0.19
## b[3,2]          -1.01    0.01   0.59   -2.21   -1.40   -1.00   -0.61    0.12
## b[4,1]          -0.06    0.00   0.02   -0.10   -0.07   -0.06   -0.04   -0.02
## b[4,2]          -0.12    0.00   0.02   -0.16   -0.13   -0.12   -0.10   -0.08
##               n_eff Rhat
## b[1,1]         2022    1
## b[1,2]         1934    1
## b[2,1]         2701    1
## b[2,2]         2579    1
## b[3,1]         2835    1
## b[3,2]         2514    1
## b[4,1]         2122    1
## b[4,2]         1978    1
##  [ reached getOption("max.print") -- 759 行を無視しました ]
##
## Samples were drawn using NUTS(diag_e) at Sun May 31 00:51:09 2020.
## For each parameter, n_eff is a crude measure of effective sample size,
## and Rhat is the potential scale reduction factor on split chains (at
## convergence, Rhat=1).

R console上でfit0の中身を確認すると、各MCMCサンプルの要約統計量の他にn-eff、Rhatが出力されます。

n-eff
Stanが自己相関等から判断した実行サンプルサイズです。ある書籍には分布の推定・統計量の算出のために100程度以上あることが望ましいと紹介されています。
標本自己相関がラグを大きくしてもなかなか減衰しない場合、MCMCサンプルは過去の値に長く依存しており、不変分布である事後分布に関する推論には効率が悪い、ということのようです。Stan開発者はこちらのページでn-effの定義をしています。私もまだちゃんと読んでいないのでいつか読みたいです。

Rhat( $\hat{R}$ )
こちらはMCMCが収束したかを表す一つの指標です。
Rhatについては少し詳しく紹介しておきます。
いまchain数を $M$ 、iterationを $n$ とし、chain毎に $n$ 個の標本 $θ^{(i, t)}$ を発生させたとします $(i = 1, 2, \dots, M, t = 1, 2, \dots, n)$ 。
このとき、 $g (θ^{(i, t)})$ の分散 $σ_{g}^{2}$ は、

${\tilde{σ}}_{B W}^{2} = \frac{(n - 1) {\tilde{σ}}_{w}^{2} + {\tilde{σ}}_{B}^{2}}{n}$ ${\tilde{σ}}_{W}^{2} = \frac{1}{M} \sum_{i = 1}^{M} s_{g_{i}}^{2}, s_{g_{i}}^{2} = \frac{\sum_{t = 1}^{n} ((g (θ^{(i, t)})) - {\bar{g}}_{i})^{2}}{n - 1}$ ${\tilde{σ}}_{B}^{2} = n \frac{\sum_{i = 1}^{M} ({\bar{g}}_{i} - \overset{ˇ}{g})}{M - 1}, {\bar{g}}_{i} = \frac{1}{n} \sum_{t = 1}^{n} g (θ^{(i, t)}), \overset{ˇ}{g} = \frac{1}{M} \sum_{i = 1}^{M} {\bar{g}}_{i}$

の ${\tilde{σ}}_{B W}^{2}, {\tilde{σ}}_{W}^{2}, {\tilde{σ}}_{B}^{2}$ のいずれでも推定できます。

MCMC標本の自己相関が高く、不変分布である事後分布への収束が遅い場合、 $s_{g_{i}}^{2}$ (=1chain内の不偏分散)は真の分散 $σ_{g}^{2}$ よりも小さくなり、したがって ${\tilde{σ}}_{W}^{2}$ ( $s_{g_{i}}^{2}$ の平均)も小さくなります。
一方、各連鎖の動きが緩慢で事後分布の一部でしかサンプリングされていないときは、 ${\tilde{σ}}_{B}^{2} / n$ (=各chainの標本平均の不偏分散)が大きくなり、したがって ${\tilde{σ}}_{B}^{2}$ も大きくなります。

そこで、下記式で $\hat{R}$ を定義すると、 $\hat{R}$ が1に近いかどうかでMCMCの収束を判断することが出来ます。Galman(1996)は $\hat{R}$ が1.1~1.2以下になれば収束したと実用上考えてよいとしているそうです。

$\hat{R} = \frac{{\tilde{σ}}_{B W}^{2}}{{\tilde{σ}}_{W}^{2}}$

今回は全係数でRhatが1ですので、MCMCは収束したと判断します。

モデルの係数に着目

R console上でfit0の中身を確認したとき、係数の要約統計量が以下のように算出されていました。

options(max.print = 80)
fit0

## ～省略～
##
##                  mean se_mean     sd    2.5%     25%     50%     75%   97.5%
## b[1,1]           2.89    0.03   1.16    0.62    2.11    2.90    3.66    5.12
## b[1,2]           5.36    0.03   1.13    3.17    4.61    5.32    6.14    7.57
## b[2,1]          -0.54    0.01   0.45   -1.41   -0.83   -0.53   -0.24    0.33
## b[2,2]           0.32    0.01   0.48   -0.64    0.00    0.31    0.64    1.28
## b[3,1]          -1.19    0.01   0.52   -2.27   -1.53   -1.19   -0.84   -0.19
## b[3,2]          -1.01    0.01   0.59   -2.21   -1.40   -1.00   -0.61    0.12
## b[4,1]          -0.06    0.00   0.02   -0.10   -0.07   -0.06   -0.04   -0.02
## b[4,2]          -0.12    0.00   0.02   -0.16   -0.13   -0.12   -0.10   -0.08

事後分布の代表値とし上の中央値(50%列の値)も用いられますが、ここでは最尤法による結果との整合性を確認するためMAP推定値も算出してみます。事後分布のMAP推定値が最尤推定による結果と理論的に一致することについては以前の記事を参照してください。

b_MAP <- apply(posterior_fit0_2$b, c(2,3), function(x){
mode_x <- density(x)$x[which.max(density(x)$y)]
})
colnames(b_MAP) <- c("general","vocation")
t(b_MAP)

##           Intercept  sesmiddle   seshigh       write
##  general   2.898204 -0.5127911 -1.224067 -0.05841702
##  vocation  5.059521  0.2740113 -1.028054 -0.11497210

一方、以前の記事でmultinom()を用いて同じ分析を行った結果が以下です。

## Call:
## multinom(formula = prog2 ~ ses + write, data = ml)
##
## Coefficients:
##          (Intercept)  sesmiddle    seshigh      write
## general     2.852198 -0.5332810 -1.1628226 -0.0579287
## vocation    5.218260  0.2913859 -0.9826649 -0.1136037
##
## Std. Errors:
##          (Intercept) sesmiddle   seshigh      write
## general     1.166441 0.4437323 0.5142196 0.02141097
## vocation    1.163552 0.4763739 0.5955665 0.02221996
##
## Residual Deviance: 359.9635
## AIC: 375.9635

## 両側Z検定の実行
z <- summary(test)$coefficients/summary(test)$standard.errors
p <- (1 - pnorm(abs(z),0,1))
p

##           (Intercept) sesmiddle    seshigh        write
## general  7.238305e-03 0.1147190 0.01186928 3.409451e-03
## vocation 3.649650e-06 0.2703765 0.04947488 1.588023e-07

事後分布のMAP推定値とmultinom()による結果のcoefficients:を比較してみると、おおよそ一致していることがわかります。多少のずれはモンテカルロ誤差などの影響の範囲内と考えます。このことから、最尤推定に基づく方法とベイズ統計からのアプローチの整合性が確認できました。

multinom()の際には有意差検定を実行していましたので、今回もパラメータが0より大きい(小さい)確率(Bayesian p-value)を算出しておきます。

posterior_fit0_2 <- rstan::extract(fit0)

p_coef <- apply(posterior_fit0_2$b,c(2,3), function(x){
  sum(x > 0)/length(x)
})
rownames(p_coef) <- c("Intercept","sesmiddle","seshigh","write")
colnames(p_coef) <- c("general","vocation")
t(p_coef)

##            
##           Intercept sesmiddle seshigh  write
##  general    0.99325   0.11125   0.009 0.0015
##  vocation   1.00000   0.74550   0.041 0.0000

以上の結果の解釈はmultinom()の時より直感的で、例えば $b_{14}$ に着目すると、

$b_{14}$ は95%の確率で-0.10から-0.02の値をとる。また中央値は-0.06である。
$b_{14}$ が0よりも大きい確率は0.15%である

というように解釈できます。

これを知ったかめきちの感想が以下になります。

multinom()の時と比べてずっと分かりやすくないですか？？＞🐢

全結果を数式で表現しておきます(Bayesian p-valueに基づいて $^{* * *}$ ：0.1%有意、 $^{* *}$ ：1%有意、 $^{*}$ ：5%有意)。

$\frac{P (p r o g = g e n e r a l)}{P (p r o g = a c a d e m i c)} = e x p ({2.90}^{* * *} - 0.53 (s e s = m i d d l e) - {1.19}^{* *} (s e s = h i g h) - {0.06}^{* *} w r i t e)$

$\frac{P (p r o g = v o c a t i o n)}{P (p r o g = a c a d e m i c)} = e x p ({5.32}^{* * *} - 0.31 (s e s = m i d d l e); - {1.00}^{*} (s e s = h i g h) - {0.12}^{* * *} w r i t e)$

オッズ比の変量に着目

オッズ比の変量(説明変数が変化すると、オッズ比は何倍になるか)についても確認しておきます。こちらは事後分布の要約統計量ではなく、事後分布自体を視覚的に見てみることにします。また通常切片項は解釈に用いないため、図の描画では割愛します。

plot_title <- ggtitle("Posterior distribution", "with medians and 95% intervals")

mcmc_areas(as.matrix(fit0),
           pars = c("ratio[2,1]","ratio[3,1]","ratio[4,1]","ratio[2,2]","ratio[3,2]","ratio[4,2]"),prob=0.95, area_method = "equal height") +
           plot_title+ theme_bw(base_size=12)

上図の事後分布に表現された中央値、95%信頼区間を下で算出しておきます。

ratio_median <- apply(posterior_fit0_2$ratio, c(2,3), median)
ratio_quant <- apply(posterior_fit0_2$ratio, c(2,3), quantile, prob=c(0.025, 0.975))
ratio_general <- rbind(ratio_median[,1], ratio_quant[,,1])
ratio_vocation <- rbind(ratio_median[,2],ratio_quant[,,2])
rownames(ratio_general) <- rownames(ratio_vocation) <- c("median","2.5%","97.5%")
colnames(ratio_general) <- colnames(ratio_vocation) <-  c("Intercept","sesmiddle","seshigh","write")
ratio_odds <- list(general = ratio_general, vocation=ratio_vocation)

show(ratio_odds)

## $general
##        Intercept sesmiddle   seshigh     write
## median  18.08714 0.5897972 0.3041684 0.9428201
## 2.5%     1.85266 0.2434086 0.1037669 0.9051025
## 97.5%  166.69899 1.3964119 0.8242418 0.9836004
##
## $vocation
##         Intercept sesmiddle   seshigh     write
## median  204.48713  1.369324 0.3678701 0.8901682
## 2.5%     23.69682  0.527517 0.1092642 0.8515944
## 97.5%  1940.58136  3.594567 1.1219872 0.9260589

上図で一番目立つ $r a t i o [2, 2]$ に着目すると、これは $\exp (b_{22})$ ですので、 $\frac{\frac{P (p r o g = v o c a t i o n (s e s = m i d d l e))}{P (p r o g = a c a d e m i c (s e s = m i d d l e))}}{\frac{P (p r o g = v o c a t i o n (s e s = l o w))}{P (p r o g = a c a d e m i c (s e s = l o w))}}$ の事後分布を表現しています。事後分布は95%ベイズ信頼区間内に1を含んでいますし、比較的幅が広い分布ですので、確信をもってこうだといえる結果が得られていないことがわかります。

一方で、 $r a t i o [3, 1] = \exp (b_{21})$ は幅が比較的狭く、95%ベイズ信頼区間内に1が含まれていません。このことから、 $\frac{\frac{P (p r o g = g e n e r a l (s e s = h i g h))}{P (p r o g = a c a d e m i c (s e s = h i g h))}}{\frac{P (p r o g = g e n e r a l (s e s = l o w))}{P (p r o g = a c a d e m i c (s e s = l o w))}}$ はより確信をもって1以下の代表値(MAP推定値や中央値)付近をとる、ということができます。

このように、ベイズ統計ではパラメータや求めたい値のとりうる分布を推定することができ、大変便利です。

結果の描画

最後に結果(確率に関する予測値の分布)の描画を行います。以下では各programが選ばれる確率を、事後分布の中央値を予測値として、50%ベイズ信頼区間とともに示しています。

library(ggplot2)
library(RColorBrewer)

p25 <- apply(posterior_fit0_2$pred, c(2,3), quantile, prob=c(0.25))
p50 <- apply(posterior_fit0_2$pred, c(2,3), median)
p75 <- apply(posterior_fit0_2$pred, c(2,3), quantile, prob=c(0.75))
colnames(p25) <- paste0(c("academic","general","vocation"),"_p25")
colnames(p50) <- paste0(c("academic","general","vocation"),"_p50")
colnames(p75) <- paste0(c("academic","general","vocation"),"_p75")
data1 <- data.frame(ses = rep(c("low","middle","high"),each = 41), write = x_new[,-c(1:3)],y=p50[,"academic_p50"], ymax=p75[,"academic_p75"],
                    ymin=p25[,"academic_p25"], facet="academic")
data2 <- data.frame(ses = rep(c("low","middle","high"),each = 41), write = x_new[,-c(1:3)],y=p50[,"general_p50"], ymax=p75[,"general_p75"],
                    ymin=p25[,"general_p25"], facet="general")
data3 <- data.frame(ses = rep(c("low","middle","high"),each = 41), write = x_new[,-c(1:3)],y=p50[,"vocation_p50"], ymax=p75[,"vocation_p75"],
                    ymin=p25[,"vocation_p25"], facet="vocation")


cols = RColorBrewer::brewer.pal(3,"Dark2")

data_point <- ml %>% cbind(makedummies::makedummies(ml,basal_level = T, col = "prog")) %>%
  select(c(ses, write, prog, prog_academic, prog_general, prog_vocation))

p0 <- ggplot() + theme_bw(base_size=11) + mapply(
  function(data){
    geom_ribbon(data=data, aes(x=write, ymax=ymax, ymin=ymin, fill=ses), alpha=0.5)
  },list(data1,data2,data3)
) +mapply(
  function(data){
    geom_line(data=data,aes(x=write, y=y, colour=ses))
  },list(data1,data2,data3)
) + mapply(
  function(data,n){
  geom_jitter(data=data,aes(x=write, y=data[,n], colour=ses),height=0.1, width=0, size=0.8)
},list(data.frame(data_point, facet="academic"),data.frame(data_point, facet="general"),data.frame(data_point, facet="vocation")),
  list(4,5,6)) +
  facet_grid(facet~.) + scale_colour_manual(values=cols) + scale_fill_manual(values=cols) +
  theme(legend.position = "bottom") + ylab("Probability") + labs(title = "With Rstan")

p0

multinom()による分析の際に描画した図を下に載せますが、この2つの結果はほぼ一致していることがわかります。

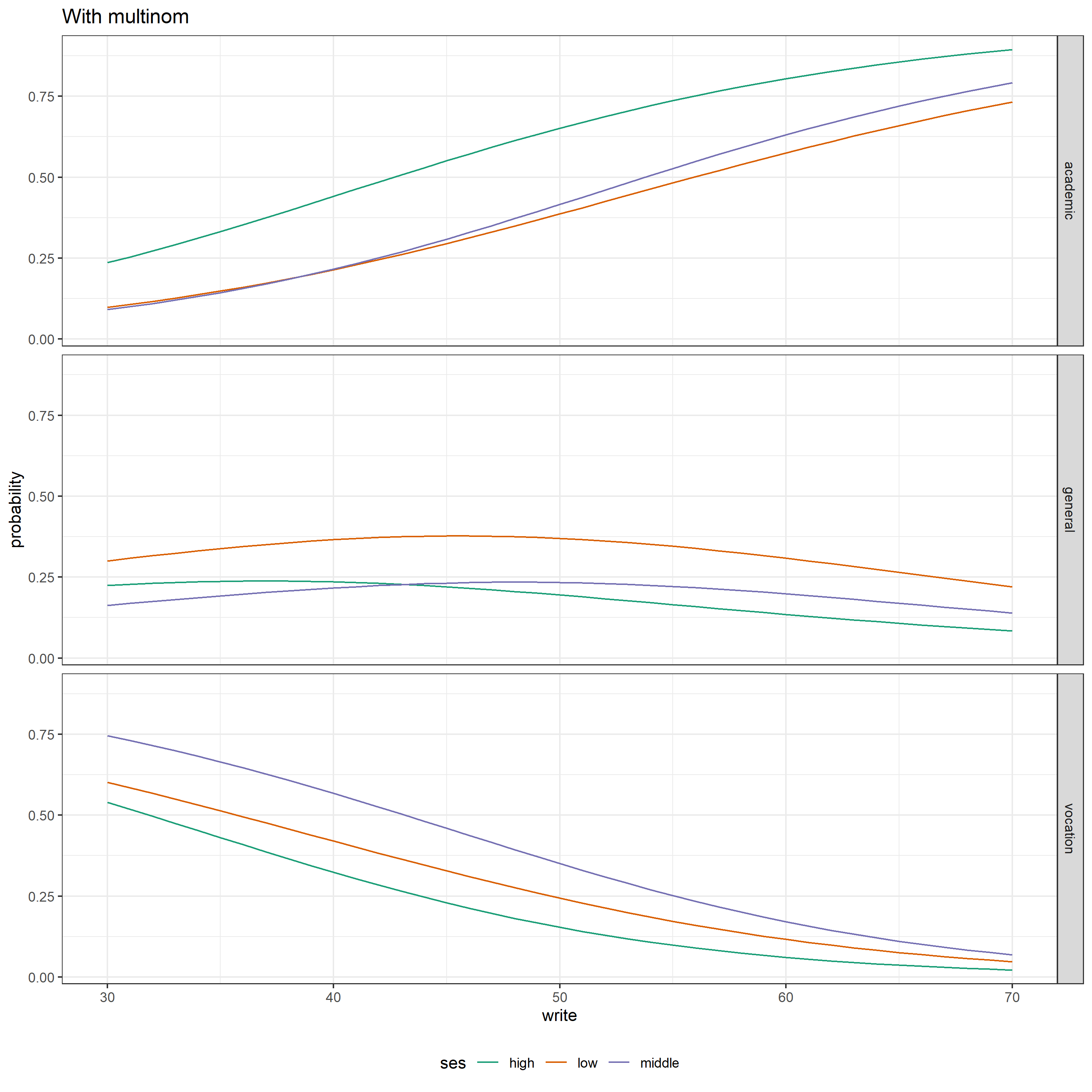
まとめ

本記事では多項ロジスティック回帰をRstanを用いて実行し、最尤法(multinom())による結果との比較を行い、ネイマン・ピアソン型統計とベイズ統計の違いを確認しました。

両者がやっていることは実質的には変わりありませんが、解釈の違いなどについては実感できたかと思います。

今後、今回の実装にさらに改良を加え、予測用のモデルを構築したいと思います。

2020.05.31 00:00

rstanを使った多項ロジスティック回帰