はじめに
本記事では今後の記事でも頻繁に扱う予定のベイズ統計について理解してもらうため、その理論を簡単に説明します。
本記事の構成は以下の通りです。
ネイマン・ピアソン型統計とベイズ統計
統計学の流派は大きくネイマン・ピアソン型統計とベイズ統計の2つが存在します。
ネイマン・ピアソン型統計
ネイマン・ピアソン型統計では、母集団のパラメータ$\theta$(母平均や母分散など)を未知ではあるが固定された値であると考え、母集団からの標本$x$を確率的な変動をもって実現した値であるととらえます。
そして、$\theta$を固定したとき、観察されたデータ$x$がどの程度生じやすいかの指標として、尤度
$$
P(x | \theta)
$$
を計算し、尤度が最も大きくなる値$\theta$を求めることで$\theta$の最尤推定量とする手法が、最尤法と呼ばれる、ネイマン・ピアソン型統計において最も重要な手法になります。
最尤推定に限らず、平均値の差の検定のような問題あっても、A群とB群の平均値に差がない($\mu_A = \mu_B$)という帰無仮説を設定することから始まり、設定した仮説のもとで、観察されたデータがどの程度の確率で起こるかをP値として求め、帰無仮説の真偽を判定します。
ベイズ統計
ベイズ統計では、ネイマン・ピアソン型統計とは対照的に、データ$x$を確定的な実現値であると考え、母集団のパラメータ$\theta$の方を確率的な分布を持った値であるとみなします。そのため、最終的に求めようとする対象は $$ P(\theta|x) $$ となります。
この$P(\theta|x)$ですが、ネイマン・ピアソン型統計の$P(x|\theta)$とは扱いが少し異なります。ベイズ統計における$P(\theta|x)$では「〇〇という条件のもと△△が得られる確率」における「〇〇」に対応する$x$が観測値として与えられています。また$P(\theta|x)$は$\theta$について積分すると1になります。このことから、$P(\theta|x)$は$x$が与えられると決定される$\theta$の確率密度関数もしくは確率質量関数ととらえることが出来ます。
一方、最尤推定における$P(x|\theta)$については、「〇〇という条件のもと△△が得られる確率」における「△△」に対応する$x$が観測値として与えられています。よって、$\theta$を1つの値に固定したとき、その値に応じて$x$の確率分布が変化することになりますが、$x$は観測値として与えられている為その分布自体が関心の対象となることはありません。より正確には、固定した$\theta$に応じて変わる$x$の確率密度関数・確率質量関数の、観測値の点に対応する値のみが関心の対象となっているといえます。
このあたり、図示すると分かりやすいので、時間を見つけて更新したいです。
ベイズ統計では、ベイズの定理と呼ばれる下記式が$P(\theta | x)$の推定に使用されます。
$$ P(\theta | x) = \cfrac{P(x | \theta)P(\theta)}{P(x)} $$
$P(\theta|x)$を$\theta$の事後分布、$P(\theta)$を$\theta$の事前分布と呼びます。$P(x | \theta)$はネイマン・ピアソン型統計で紹介した尤度で、$\theta$を特定の値としたときに実現値$x$が得られる確率を意味します。
右辺の分子$P(x)$はデータ$x$が得られる確率ですが、これは$\theta$には依存しない、かつ未知の値であるため、$P(\theta | x)$の正規化定数ととらえ、下記式に基づいて$P(\theta | x)$を計算します。
$$ P(\theta | x) \propto P(x | \theta)P(\theta) = (尤度) × (事前分布) $$
ネイマン・ピアソン型統計とベイズ統計の整合性
以上がネイマン・ピアソン型統計とベイズ統計の理論上の違いになりますが、ここで両者のアプローチの整合性について触れておきます。
事後分布$P(\theta|x)$の値が最大になる点$\hat{\theta}$はMAP推定値(maximum a posteriori estimate)と呼ばれますが、この値は$\theta$の事前分布$P(\theta)$を十分に分散が大きい正規分布や十分に幅の広い一様分布に設定することで無情報事前分布を指定すると、
$$ \newcommand{\argmax}{\mathop{\rm arg~max}\limits} \hat{\theta} = \argmax_{\theta}~P(x|\theta)P(\theta) \ = \argmax_{\theta}~ P(x|\theta) $$
が成り立ちます。このことから、$\hat{\theta}$は最尤推定値と一致することがわかります。
ネイマン・ピアソン型統計とベイズ統計の違い
ネイマン・ピアソン型統計とベイズ統計の分析上の違いをまとめておきます。
パラメータの解釈
ネイマン・ピアソン型統計ではパラメータは定数とみなします。前回の記事でも、モデルの係数はsummary(test)でCoefficients:に確定値、Std.Errorsに標準誤差が得られていました。この結果の解釈の仕方は、
「与えられたデータから推測される係数の値は(確定値)だ。ただし、同じ母集団から同じようにデータを取り直した場合、パラメータは(標準誤差)の分散をもって取得される」
となります。
一方、ベイズ統計では母集団のパラメータの分布が得られることから、
「パラメータがこの範囲である確率は何%だ」
もしくはより直接的に
「パラメータの確率密度関数の近似はこれだ」
といった解釈ができます。
この両者を比較すると、どちらが解釈しやすいでしょうか?
人間の直感で理解しやすいのは後者の場合ではないかと思います。そのため、意思決定のために統計学的な分析を行うとき、ベイズ統計を選ぶことには利点があると考えられます。
有意差問題
ネイマン・ピアソン型統計では平均値の差の検定の際などに有意確率P値に着目し、P値が$\alpha$よりも小さければ帰無仮説を棄却、そうでなければ対立仮設を採択、といった判断を行います。
実はこの有意差検定、困ったことに、標本サイズを増やせばどんなに小さな平均値間の差であっても有意な差として検出できてしまうという問題があります。
これに対し、ベイズ統計からのアプローチでは、平均値の差という母集団のパラメータの確率分布を推定し、明示することができるため、ビックデータを扱う際にも、微小な平均値の差異は本当に有意なのか？といった問題から脱却することができます。
ベイズ推定では、標本数を増やすと求めたい分布は幅が狭くなっていく(より確信を持った分布を掲示できる)ため、ネイマン・ピアソン型統計よりもビックデータを有効活用できると考えられます。
手法(最尤法とMCMC)による違い
ネイマン・ピアソン型統計では最尤法が頻繫に使用されますが、この手法は過学習に陥りやすいという問題があります。また、モデルが複雑な場合、最尤法では局所最適地に陥りやすく、最適化が困難になります。
一方、ベイズ統計では次節で説明するMCMCを利用してパラメータの分布を求めるため、上記の問題が解決できます。
マルコフ連鎖モンテカルロ法(MCMC)
ベイズ統計では、パラメータの事後分布を求めることが目標となりますが、これを解析的に求めることは難しく、不可能であることも多いです。そのため、マルコフ連鎖モンテカルロ法(Malcov Chain Monte Carlo method、以下MCMC)というアルゴリズムを用います。 MCMCは、簡単に説明するとある確率分布に従う乱数を発生させるアルゴリズムです。これまでメトロポリス法、ギブスサンプラー、ハミルトニアンモンテカルロ法等様々なアルゴリズムが提案されていますが、ここではメトロポリス法を紹介し、MCMCがどのようなアルゴリズムなのか簡単に説明します。
以下のモデルを考えます。
$$ Y[n] \sim \rm{Normal}(\mu, 1)~~~~n=1,\ldots,N $$ $$ \mu \sim \rm{Normal}(0, 100) $$
ここで、$Y$:従属変数の観測値、$X$:説明変数の観測値、$N$：サンプルサイズです。
事後確率$P(\mu|Y)$は下記式で計算できます。
$$ P(\mu | Y) \propto P(Y | \mu)P(\mu) =\left[ \prod_{n=0}^{N} \rm{Normal}(Y[n] | \mu, 1)\right] \rm{Normal}(\mu|0,100) $$
このモデルにメトロポリス法を適用した場合、以下のようなアルゴリズムになります。
[メトロポリス法]
$\mu$を任意の初期状態からはじめて、以下を繰り返す。
- $\Delta$を原点対象の確率密度から発生させる。
- サンプル候補の$\mu^{'}$を以下で定める。 $$ \mu^{'} \leftarrow \mu + \Delta $$
- サンプル候補と現在で$P(\mu|Y)$の比$r$を計算する。 $$ r \leftarrow \cfrac{\left[ \prod_{n=0}^{N} \rm{Normal}(Y[n] | \mu{'}, 1)\right] × \rm{Normal}(\mu{'}|0,100)}{\left[ \prod_{n=0}^{N} \rm{Normal}(Y[n] | \mu, 1)\right] × \rm{Normal}(\mu|0,100)} $$
- $0 \leq R < 1$の一郎乱数$R$を発生させる。$R<r$なら $$ \mu \leftarrow \mu^{'} $$ とし、そうでなければ現在の状態をそのまま次の状態とし、$\mu$を一つのmcmcサンプルとして保存する
最後の操作において、$r \geqq 1$ のとき、$\mu^{'}$は必ず採択されることになります。一方、$r < 1$のときでも確率$r$で$\mu^{'}$が採択されるところが重要で、この設定により$\mu^{'}$の局所的極大値に落ち着くことがなく、永遠にさまよい続けることになります。それでも、広い目で見ると$\mu^{'}$は(尤度)×(事前分布)が最大になる値付近に近づき、その周辺でサンプリングし続けることになります。
最後に、予測対象である$P(\mu | Y)$は、収集したMCMCサンプルの分布で近似されることになります。
Stanを用いたMCMCサンプリング
Stanは、ベイズモデリングを行うために開発された汎用的な確率的プログラミング言語です。推定計算のアルゴリズムにはハミルトニアンモンテカルロ法の一実装であるNUTSが用いられます。
MCMCによるサンプリングの様相を把握するため、例としてあるデータに対し下記のモデル $$ Y[n] \sim \mathrm{Normal}(a + bX[n], \sigma)~~~~n=1,\ldots,N $$ を適用し、確率的プログラミング言語Stanを用いてベイズ統計・MCMCを実行したときのtraceplot(MCMCサンプルの値をとった折れ線グラフ)と、MCMCサンプルの分布を以下に示します。
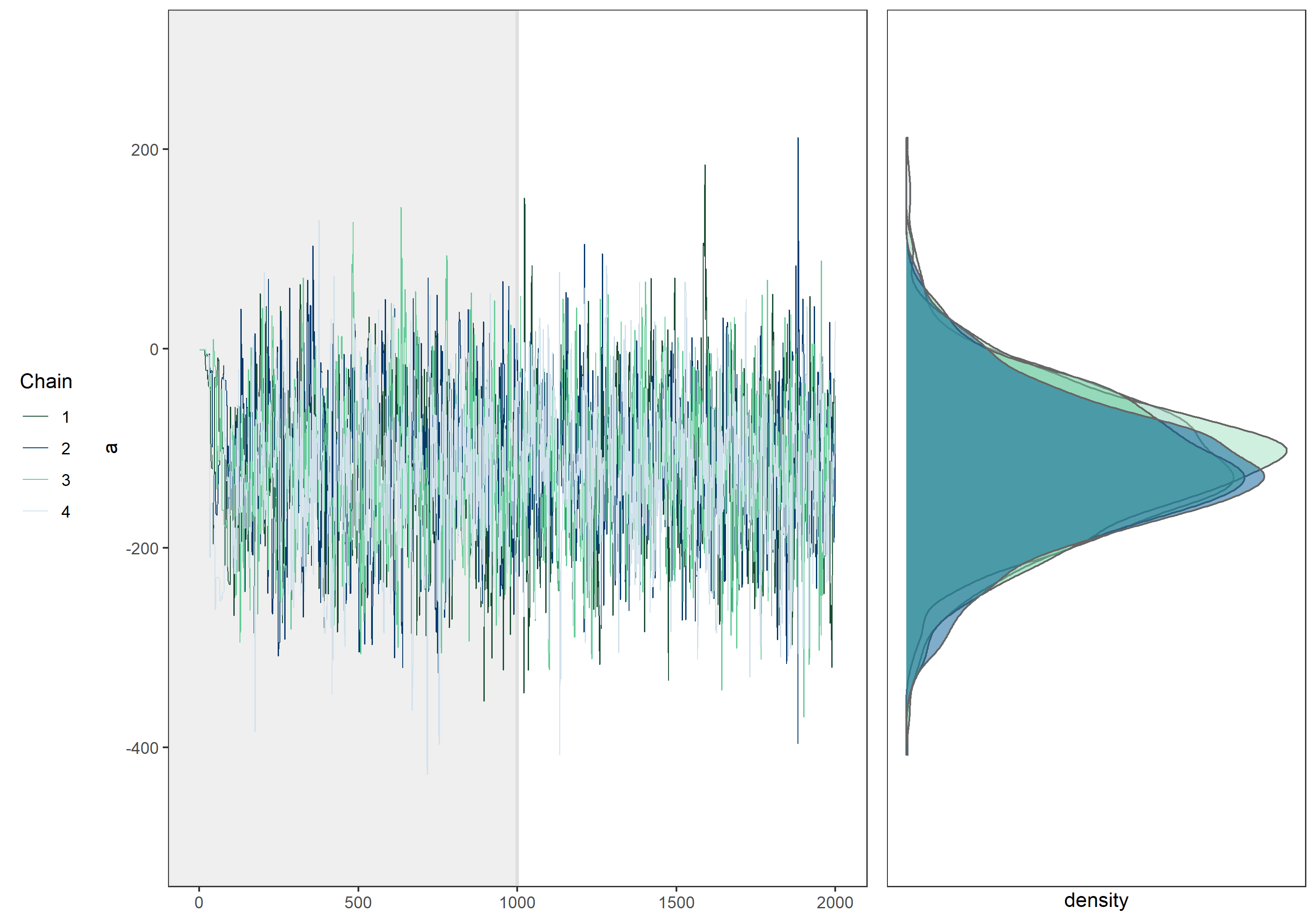
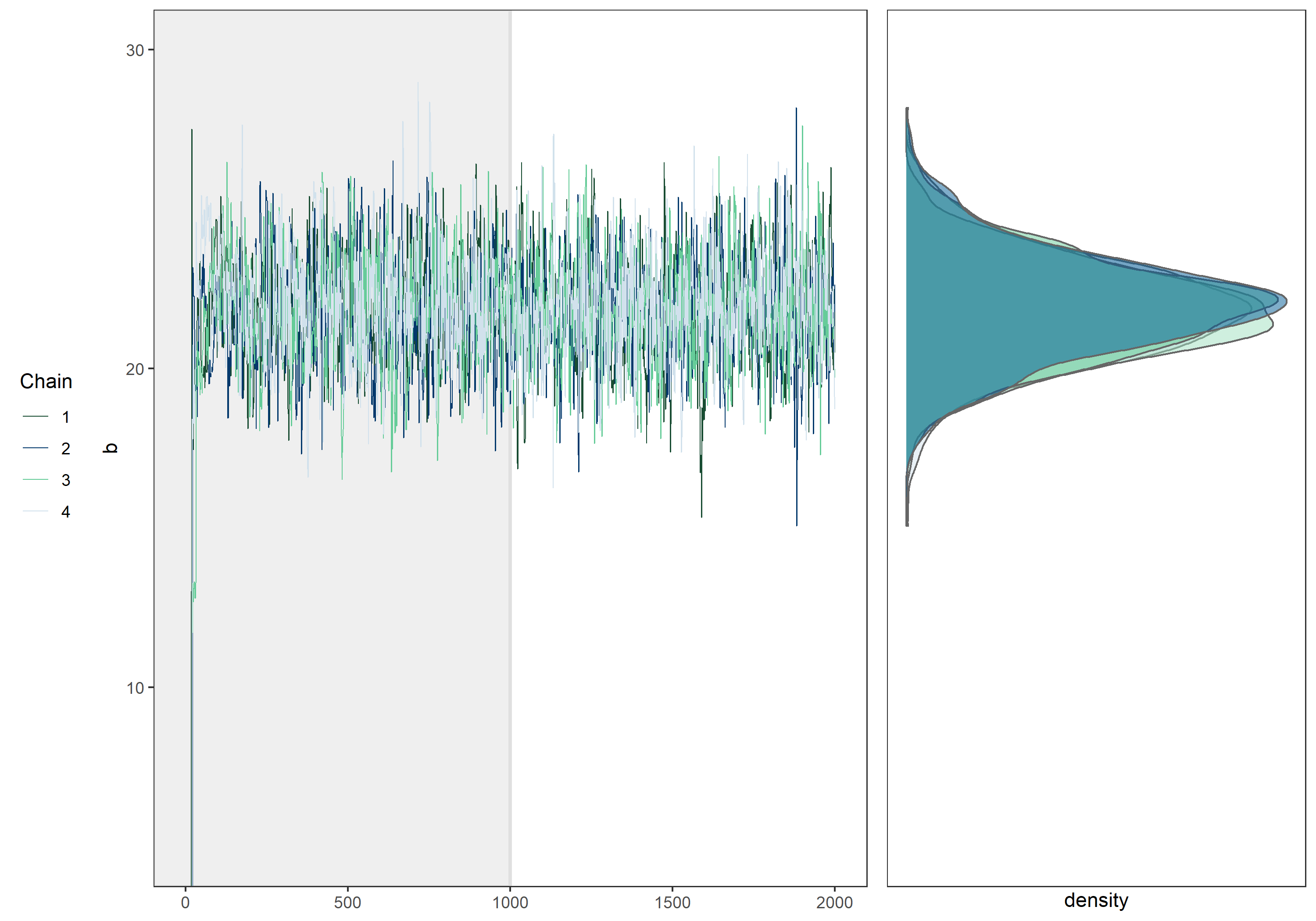
まずは左側のtraceplotを確認します。
パラメータ毎に4つの折れ線がありますが、MCMCではサンプル列をいくつか並列で実行し、事後分布への収束を確認します。この1つのサンプル列をchainと呼び、ここではchain数が4となっています。
またtraceplotの左端を注意深く観察すると、サンプリングの初期ではあさっての値がサンプリングされていることがわかります。これはランダムに設定された初期値の影響を受けている為です。 そのためサンプリング初期の値は一般にサンプルから除外されます。この期間をwarm upと呼び、warm up後のMCMCサンプルが事後分布からサンプリングされたものであると考えます。 上のtraceplotでは設定したwarm up期間を背景を濃くすることで表現しています。
traceplotを見る限り、warm up後のMCMCサンプルは初期値の影響を受けていないことから、正しいwarm up期間を設定できていると分かります。またこれ以上iterationを増やしても事後分布の形状に違いは生まれないように思われます。
次に右側のMCMCサンプルの分布を確認します。
図では4つの確率密度分布が描画されており、これらは各chain毎にwarm upを除いたMCMCサンプルから作成した確率密度分布です。4つの密度分布は微妙な差がありますが、ほぼ同じ分布であることが分かります。
ベイズ統計において求める対象は、パラメータに関する分布であり、実際の分析においては全chainのMCMCサンプルを混合し、一つの分布として扱うことになります。
今回紹介した事例では、4つのchainがほぼ同じ部分をサンプリングし続けていること、chain毎のMCMCサンプルの分布がほぼ同じであることから、このMCMCは不変分布である事後分布に収束したと考えることが出来ます。
モデルや設定によっては上のtraceplotのようにならず、各chainが一つの値に収束しない場合もあります。そのような場合はモデルを再考したりする必要があります。
まとめ
本記事ではベイズ統計について、ネイマン・ピアソン型統計と比較しつつ説明をしました。
どうしても文章ばかりの記事になってしまい、「結局何をしているの？」となってしまったかもしれません。
次回の記事では実際にデータを用いてベイズ統計による分析を実施し、ネイマン・ピアソン型統計からのアプローチとの違いを確認したいと思います。
